Energy Decomposition Analysis (EDA)
- Author:
Max Phipps, University of Southampton
- Date:
July 2016
Introduction
Energy decomposition analysis (EDA) decomposes the interaction energy (\(\Delta E\)) of an arbitrary number of non-bonded fragments into its chemical components [Phipps2015]. In the case of the ONETEP EDA [Phipps2016], based on the ALMO [Kaliullin2007] and LMO [Su2009] EDA approaches, these components are combined into a frozen density component (\(\Delta E_\mathrm{FRZ}\)) term, polarisation (\(\Delta E_\mathrm{POL}\)), and charge transfer (\(\Delta E_\mathrm{CT}\)) (as per the original ALMO EDA), as,
The frozen density component, representing the interaction of the frozen densities of the fragments and subsequent antisymmetrization, is further decomposed into its electrostatics (\(\Delta E_\mathrm{ES}\)), exchange (\(\Delta E_\mathrm{EX}\)), correlation (\(\Delta E_\mathrm{CORR}\)), and Pauli repulsion (\(\Delta E_\mathrm{REP}\)) terms as,
In the ONETEP implementation, the correlation term is further partitioned into its frozen (\(\Delta E_\mathrm{FRZ-CORR}\)) and Pauli repulsion (\(\Delta E_\mathrm{REP-CORR}\)) terms as,
These terms may be recombined to obtain the full correlation energy term.
The total interaction energy is expressed in its decomposed form as,
Performing EDA calculations in ONETEP
There are two approaches to performing energy decomposition analysis (EDA) calculations in ONETEP:
All-In-One (1S) This approach involves creating a single input file with all the necessary information to complete an EDA calculation (
TASK EDA).Designed for smaller systems.
Three-Stage Fragment-to-Supermolecule (3S) This approach involves three stages. Firstly NGWF tightboxes and density kernels for the fragments are optimised and written to disk. Next the fragment states are superposed to the supermolecule to prepare the supermolecule data (
TASK EDA_PREP). Finally the EDA calculation is ran using this supermolecule-prepared data (TASK EDA).Designed for larger protein-ligand type EDA calculations.
Both approaches are equivalent and produce identical results. The choice of whether to use the 1S or 3S approach is usually determined by system size and parallelisation requirements (please see section [sect:ParallelisationReq]). Further details of calculations using these two approaches and a list of the EDA-specific keywords and descriptions are provided below:
All-in-One
The all-in-one (1S) approach is the default EDA calculation
configuration, and is ran by simply setting the TASK keyword to
EDA. In addition to the standard input keywords and blocks, the
EDA_IATM block is necessary to perform ONETEP EDA calculations. This
block defines the fragment atoms (referenced to the atom definitions in
POSITIONS_ABS), and the fragment charges. Atoms of the supermolecule
are arranged in the POSITIONS_ABS block by concatenation of the
fragment atoms, using their nuclear coordinates found in the
supermolecule. For example, if a supermolecule system comprising the
fragments \(H_2O\) (atoms 1 to 3), \(OH^-\) (atoms 4 to 5), and
\(Na^+\) (atom 6) is defined in the POSITIONS_ABS block,
%block POSITIONS_ABS
O 17.16973430 19.79077059 17.26422010
H 16.00000000 19.22196603 16.00000000
H 18.57568311 18.64371289 17.26799954
O 21.16270452 17.46075058 18.04467287
H 22.06598884 16.00000000 17.45886087
Na 20.73940810 20.59012052 20.33500884
%endblock POSITIONS_ABS
then the fragment data necessary for the EDA calculation is input as,
%block EDA_IATM
!N_at Charge
3 +0
2 -1
1 +1
%endblock EDA_IATM
Three-Stage
The 3S EDA has been developed to work easily with EDA directory
structures, with fragment calculations being performed in separate
folders. These data directories are specified in the input file using
the EDA_FRAG and EDA_SUPER blocks as will be discussed below. In
our EDA calculation example of a supermolecule comprising three
fragments provided below, the following directory structure is used:
It is noted that the user is not limited to three fragments , and that the folder names given above are for example purposes only and any folder and input file names may be used.
In all three stages, it is necessary to ensure that the system parameters are kept at constant values. For example, it is unwise to modify the NGWF radii or box sizes between the calculation stages. It is also important to ensure atomic orderings in the input file are consistent, i.e. that the orderings of atoms within each of the fragments do not change between the different calculation stages.
Stage 1
The first stage simply involves the user writing converged fragment data to disk. For each fragment comprising the supermolecule, a separate input file is constructed with the following parameters set:
write_denskern T
write_tightbox_ngwfs T
TASK SINGLEPOINT
Running these calculations will result in fragment ‘.dkn’ and
‘.tightbox_ngwfs’ files being written to disk. In our example, the
three fragment calculation are ran in the directories
STAGE1/FRAG01/, STAGE1/FRAG02/, and STAGE1/FRAG03/ using the
input filenames ‘frag01.dat’, ‘frag02.dat’, and ‘frag03.dat’ for the
respective fragments 1, 2, and 3.
Stage 2
The input file for the second stage is prepared by including the
parameters EDA_READ_FRAGS T and TASK EDA_PREP. Running ONETEP
with this input file will result in the converged fragment data being
loaded in and combined to produce the supermolecule complex data
(‘.eda’, ‘.dkn’ and ‘.tightbox_ngwfs’ files) necessary for stage three.
These fragment files’ names are set via the EDA_FRAG block, e.g. for
a three fragment system:
%block EDA_FRAG
frag1prefix
frag2prefix
frag3prefix
%endblock EDA_FRAG
where frag1prefix, frag2prefix and frag3prefix are the
filename prefixes that will result in loading of the ‘.dkn’ and
‘.tightbox_ngwfs’ files for the three fragments that were converged in
stage one. In our example, we assume the second stage calculation is
performed in the directory STAGE2/ with the input filename
‘stage2.dat’. In this case the block would appear in the input file as,
%block EDA_FRAG
../STAGE1/FRAG01/frag01
../STAGE1/FRAG02/frag02
../STAGE1/FRAG03/frag03
%endblock EDA_FRAG
Stage 3
The third stage is performed by including the parameters
EDA_READ_SUPER T and TASK EDA in the input file. As described
earlier for the 1S approach, it is necessary for the user to define the
fragment atoms and charges using the EDA_IATM block. On running
ONETEP with this input file, the ‘.dkn’, ‘.tightbox_ngwfs’ and ‘.eda’
files for the supermolecule prepared from stage two will be loaded.
These files’ names are set via the EDA_SUPER block, e.g.
%block EDA_SUPER
supermoleculeprefix
%endblock EDA_SUPER
where supermoleculeprefix is the filename prefix that will result in
loading of the ‘supermoleculeprefix.dkn’,
‘supermoleculeprefix.tightbox_ngwfs’, and ‘supermoleculeprefix.eda’
files. In our example, where the third stage calculation is performed in
the directory STAGE3/ with the input filename ‘stage3.dat’, the
block would appear as,
%block EDA_SUPER
../STAGE2/stage2
%endblock EDA_SUPER
Continuation
Continuation of supermolecule-stage EDA calculations (stage three of the
3S EDA) is controlled using the EDA_CONTINUATION keyword.
Continuation files are written to disk within the current working
directory when the value of the EDA_WRITE logical keyword is set to
true, and continuation files are read by setting the
EDA_CONTINUATION logical keyword to true.
It is recommended that the storage of continuation data should be kept
separate to the TASK EDA_PREP task calculation data of stage two.
This is achieved by performing the stage three calculation in a separate
directory to the stage two calculation. This is because the EDA data
produced from the TASK EDA_PREP calculation produces a reference to
the frozen state which the NGWFs and density kernel will be reset to in
a large proportion of EDA calculation cases.
EDA schematic
An example EDA calculation and directory structure is provided in Fig. 7.
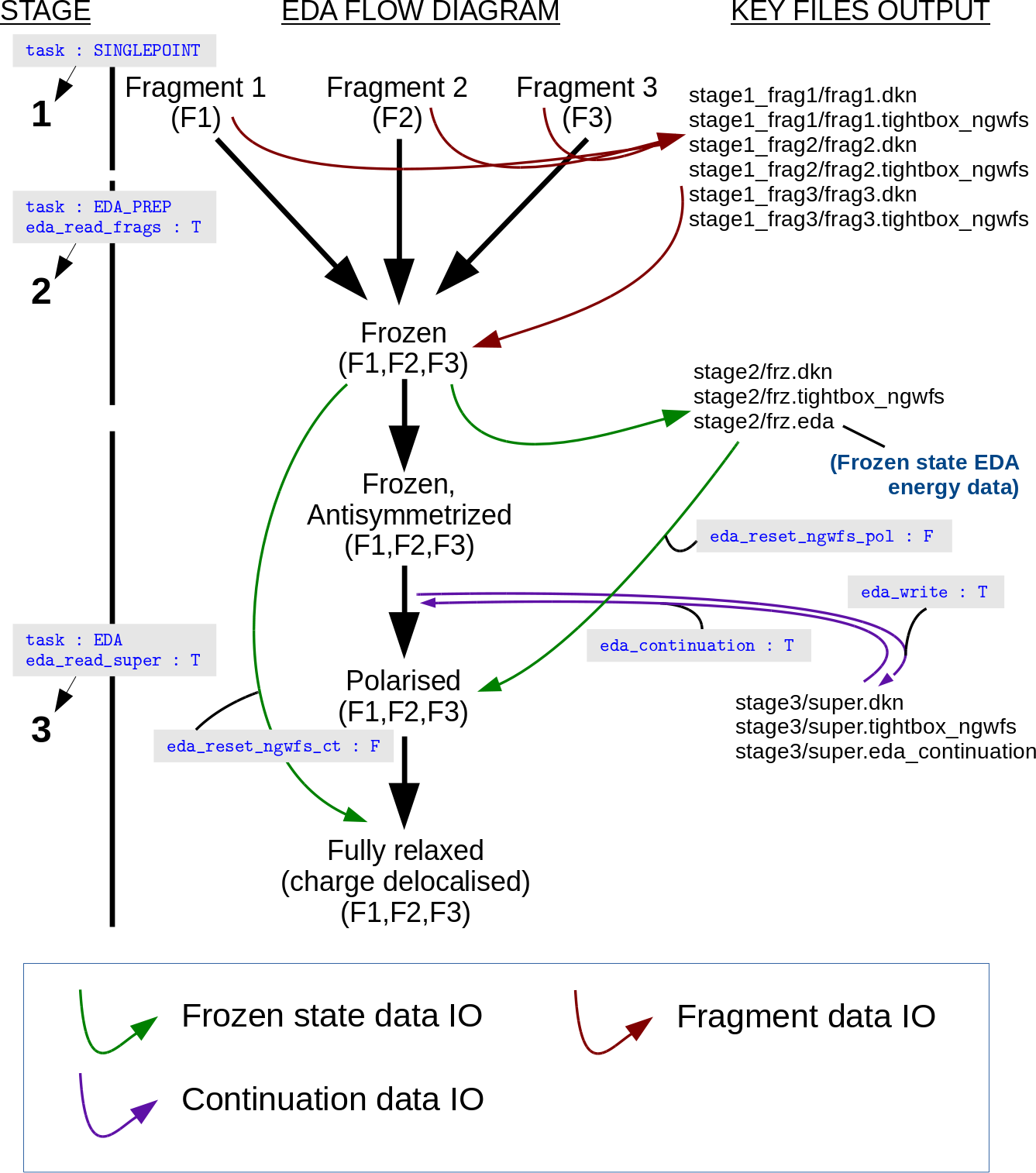
Fig. 7 An example 3S EDA calculation (data IO flows are represented by arrows).
Additional functionality
Further details of the EDA functionalities is given below:
Fragment-wise polarisations
EDA_FRAG_ISOL_POL logical keyword. Also computed is a ‘higher
order’ polarisation contribution that quantifies the difference
between the individual fragment polarisation total and the full
polarisation energy, i.e.\[\begin{aligned} \Delta E_\textrm{POL,HO} = \sum_{A\in \textrm{X}}^{N_\textrm{frag}} \Delta E_\textrm{POL(\textit{A})} - \Delta E_\textrm{POL}\end{aligned}\]
Fragment pair-wise delocalisations
EDA_FRAG_ISOL_CT logical
keyword.It is possible to calculate fragment pair delocalisation energies by combining fragments within the SCF-MI optimisation. For example, if we consider a system of interacting \((H_2O)_3\), the delocalisation between any two water molecules is calculated by subtracting the SCF-MI energy of a combined \((H_2O)_2\) ‘fragment’ interacting with \(H_2O\) from the SCF-MI energy of the system with the \((H_2O)_2\) ‘fragment’ partitioned into its two \(H_2O\) constitutents.
Density visualisation
Obtaining electron density (ED) files for visualisation of the EDA
frozen, polarisation and fully electronically relaxed states can be done
using the WRITE_DENSITY_PLOT logical keyword. The output densities
are identified by the ‘_ed_’ filename string.
Filename String |
Summary |
|---|---|
xxx_eda_frzidem_ed_density.cube |
The ED of the frozen state. |
xxx_eda_pol_iii_ed_density.cube |
The ED of fragment iii electronically polarised in the field of all other fragments. |
xxx_eda_pol_ed_density.cube |
The ED of the fully electronically polarised state. |
xxx_eda_relaxed_ed_density.cube |
The ED of the fully electronically relaxed state. |
Table: The EDA electron density (ED) filename extension descriptions (filename root is denoted by xxx).
Visualisation of the density changes during the EDA polarisation and
charge transfer processes via electron density difference (EDD)
calculations are obtained using the EDA_DELTADENS logical keyword.
The output densities are identified by the ‘_edd_’ filename string.
Filename String |
Summary |
|---|---|
xxx_pol_iii_edd_density.cube |
The electronic polarisation EDD of fragment iii in the field of all other fragments. |
xxx_eda_pol_higher_order_edd_density.cube |
The higher order electronic polarisation EDD (of the individual fragment-polarised states to the fully polarised state). |
xxx_eda_pol_edd_density.cube |
The fully electronically polarised EDD state. |
xxx_eda_ct_edd_density.cube |
The charge transfer EDD. |
Table: The EDA electron density difference filename extension descriptions (filename root is denoted by xxx).
Both ED and EDD functionalities are compatible with fragment-specific
(see previous section) EDA calculations.
Note: electron density differences are currently not computable when the
EDA_CONTINUATION keyword is set to true. In this case, the edd_cube
utility may be used along with the ED cube files produced using the
WRITE_DENSITY_PLOT logical keyword to calculate EDD files
independently of ONETEP (see ‘Additional utilities’ section).
Parallelisation
Parallelisation requirements
The 1S calculation has a parallelisation strategy with restricted maximum possible number of MPI processes, \({N_\mathrm{proc,max}}\),
where \(A\) and \(B\) are fragments comprising a supermolecule \(AB\). For example in the case of a water dimer \({N_\mathrm{proc,max}}= 3\).
The 3S EDA allows the user to take full advantage of the parallelisation strategy during the supermolecule stage three, i.e.
where \({\mathrm{S}}\) is the stage number. For example in the case of a water dimer \({N_\mathrm{proc,max}}= 6\) during the supermolecule stage three (\({\mathrm{S}}\)=3).
ScaLAPACK
The current EDA implementation requires explicit calculation and manipulation of the fragment MO eigenvectors. The ONETEP EDA implementation is compatible with the LAPACK [Anderson1999] and ScaLAPACK [Blackford1997] packages, and has been interfaced to the DSYGVX and PDSYGVX eigensolvers. Compilation with the ScaLAPACK solver is enabled at compilation time using the -DSCALAPACK flag. Use of this package provides significant speed-ups by parallelised computation of the eigenvectors required.
The threshold tolerance to which the eigenvectors are orthogonalised is
specified by the eigensolver_abstol keyword. It has been observed
that the eigensolver may require tighter than the default thresholds.
This parameter can be modified in the input, e.g.
eigensolver_abstol = 1.0E-12.
Additional utilities
- utils/edd_cube.F90
This utility calculates the electron density difference between two ‘.cube’ volumetric data files Usage: ./edd_cube cubein1 cubein2 cubeout, where n(cubeout) = n(cubein1) - n(cubein2)
[Phipps2015] Maximillian J. S. Phipps, Thomas Fox, Christofer S. Tautermann, and Chris-Kriton Skylaris. Energy decomposition analysis approaches and their evaluation on prototypical protein-drug interaction patterns. Chem. Soc. Rev., 44:3177–3211, 2015.
[Phipps2016] Maximillian J. S. Phipps, Thomas Fox, Christofer S. Tautermann, and Chris-Kriton Skylaris. Energy decomposition analysis based on absolutely localised molecular orbitals for large-scale density functional theory calculations in drug design. (Submitted), 2016.
[Khaliullin2007] R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell, and M. Head-Gordon. J. Phys. Chem. A, 111:8753–8765, 2007.
[Su2009] Peifeng Su and Hui Li. Energy decomposition analysis of covalent bonds and intermolecular interactions. J. Chem. Phys., 131(1):014102, 2009.
[Anderson1999] E. Anderson, Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen. LAPACK Users’ Guide. Society for Industrial and Applied Mathematics, Philadelphia, PA, third edition, 1999.
[Blackford1997] L. S. Blackford, J. Choi, A. Cleary, E. D’Azevedo, J. Demmel, I. Dhillon, J. Dongarra, S. Hammarling, G. Henry, A. Petitet, K. Stanley, D. Walker, and R. C. Whaley. ScaLAPACK Users’ Guide. Society for Industrial and Applied Mathematics, Philadelphia, PA, 1997.