Geometry Relaxation

Author:

Loukas Kollias, University of Southampton, United Kingdom

Author:

Chris-Kriton Skylaris, University of Southampton, United Kingdom

Date:

November 2022

Introduction to geometry relaxation

Geometry relaxation is a process that moves the positions of atomic nuclei to their equilibrium values in a system. This system can be a chemical structure of higher organisation, e.g., a molecule, a cluster of molecules, or a crystal lattice. It is often called geometry optimisation as it is an optimisation process, where the objective function is the total energy of the system. More elaborately, it is a process that searches for a solution to a minimisation problem, i.e., minimise the total energy that is a function of the atomic coordinates. In place of atomic coordinates, we usually consider the positions of the nuclei of atoms in the system. This is performed in an iterative fashion and a candidate solution is provided at every iteration that is called a “step”. At every step, the optimisation algorithm dislocates the positions of the nuclei then it optimizes the electronic structure, and finally it calculates the total energy of the chemical structure. Consequently, a geometry optimisation is a series of single point energy calculations that completes when certain convergence criteria are met. In ONETEP, geometry relaxation (optimisation) is invoked by setting the \(\mathrm{TASK}\) variable in the input file as,

\[\begin{aligned} \mathrm{task:\ GeometryOptimization} \end{aligned}\]

Potential Energy Surface

The potential energies, E, of all possible configurations \((\mathbf{R}_{A}, \mathbf{R}_{B}, \ldots, \mathbf{R}_{N})\) of the atoms in the system lie on a surface. This is called the potential energy surface (PES), and it is characterised by the equation below,

(65)\[ \begin{aligned} E=E(\mathbf{R}_A, \mathbf{R}_B, \ldots, \mathbf{R}_N) \end{aligned}\]

The PES is the search domain of the optimisation algorithm, even though most geometry relaxation methods search in a region close to the initial guess structure provided by the user. Each point on the PES is associated with a value of the potential energy and a specific configuration of atoms. The initial guess geometry can be set in various ways, e.g., from experiment or based on a crystal lattice. This structure is now a point on the PES and has an associated energy We need to navigate the PES so that we find points of lower energy, hence more stable configurations compared to the initial one.

Local Optimisation

At the first step, updated atomic positions are calculated using an optimisation method (these are discussed in section 4). The first and second derivatives of the energy, E, with respect to atomic (nuclear) positions, \(\mathbf{R}\), are often calculated to estimate the next point. We remind the reader that the first derivative is related to the forces on each atom as a result of its interaction with other atoms in the system. This is a \(3N\) matrix, where \(N\) is the number of atoms in the system it has the form [Scherlis2006],

(66)\[ \begin{aligned} \mathbf{F}_{A}=-\frac{dE}{d\mathbf{R}_A} \end{aligned}\]

where the nuclear coordinates of an atom A that belongs to the system in Cartesian space are: \(\mathbf{R}_{A}=(x_{A},y_{A},z_{A})\). If the net forces on the atoms are zero, then we have an extremum. Then we need to calculate the second derivative to investigate if this is a minimum (stable structure) or a maximum (transition state). The Hessian matrix possesses information about the second derivatives, hence it is frequently called the force constant matrix. This is a \(3N\times 3N\) matrix, and it can be written in the following form for any atoms A, B in the system,

(67)\[ \begin{aligned} \mathbf{H}_{AB}=\frac{\partial^{2}E}{\partial{\mathbf{R}_A} \partial {\mathbf{R}_B}} \end{aligned}\]

This calculation is important to examine if this point is a minimum. To do this, vibrational frequencies are calculated from the Hessian [Schlegel2011]. A minimum is characterised by a net zero force and positive vibrational frequencies. In simple terms, the minimum is located where the first derivative is zero and the second derivative (that is relevant to the local curvature) is positive. Consequently, one needs to calculate the energy and its first and second derivatives to investigate if a point on the PES is a minimum.

By default, the positions of all nuclei are modified during optimisation. Nevertheless, we can exclude a subset of the nuclei of the system from the optimisation. This way we can keep the positions of certain nuclei constant, if needed, even when positions of other nuclei are changed.

Convergence Criteria

There are a few criteria that can be examined to assess whether the geometry relaxation has converged to a local minimum structure. These include criteria concerning the energy and the net forces on atoms in the system. Additionally, the geometry relaxation can be stopped if a certain number of steps has been made regardless of the energy and forces in the final structure. This is not really a convergence criterion but it is important to be able to stop the process for a number of reasons which are discussed later in this section.

Force tolerance

Atomic positions need to be relaxed as the net force on each atom should be zero. Practically, it is difficult, if at all possible, to have a net zero force on every atom. Consequently, this process minimizes the magnitude of the net force on each atom so that it approaches zero as much as possible, and within a certain tolerance. The default force tolerance is 0.002 \(E_{H}\:a_{0}^{-1}\). This criterion can be modified by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_force\_tol: [VALUE]\:[UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_force\_tol: 0.051422\:eV/ang}\\ & \mathrm{or}\\ & \mathrm{geom\_force\_tol: 0.001\:Ha/bohr}\\ & \mathrm{or}\\ & \mathrm{geom\_force\_tol: 0.001} \end{aligned}\end{split}\]

if units are not specified, they are thought to be \(E_{H} a_{0}^{-1}\).

Maximum number of steps

Another criterion that can be assessed to stop the relaxation process is the maximum number of steps to be made. The user can have both criteria, so if any of those is satisfied after a certain step, then the process is terminated. The maximum number of steps does not guarantee a minimum energy structure, but it is a good check to stop the optimisation if it does not descend the PES in a satisfactory way or if the time of the calculation is limited. In any case, it will provide us with a candidate structure after a certain number of steps given an initial guess and a specific optimisation algorithm. This criterion can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_max\_iter: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_max\_iter: 100} \end{aligned}\end{split}\]

if this is not specified by the user in the input file, then its default value is 50. This means that 50 geometry relaxation steps will be performed at most. Fewer steps will be performed if other criteria, such as force, energy tolerance, are satisfied before that.

Convergence window

The convergence window is the number of steps where all the criteria set for the geometry relaxation must be satisfied to declare convergence. The default value is 2 steps. This is recommended to achieve a balance between accuracy and efficiency. This criterion can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_convergence\_win: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_convergence\_win: 3} \end{aligned}\end{split}\]

Energy tolerance

Another convergence criterion that can be specified by the user is the energy tolerance. This tells the geometry relaxation to stop if the difference between the maximum and minimum energies per atom over \(\mathrm{geom\_convergence\_win}\) steps is less than this value. The default value is \(10^{-6} E_{H}\). This criterion can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_energy\_tol: [VALUE]\: [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_energy\_tol: 1e-7\:Ha}\\ & \mathrm{or}\\ & \mathrm{geom\_energy\_tol: 2.72e-6\:eV}\\ \end{aligned}\end{split}\]

Displacement tolerance

Another way to check if the geometry relaxation has converged is to assess the maximum displacement of the positions of the nuclei. In practice, we calculate the set of distances of nuclei between two consecutive steps. If the largest value in this set is equal to or less than the tolerance, then the maximum distance that an atom has been displaced is considered small enough to tell the optimisation to stop. In other words, atoms have not moved considerably between two consecutive steps, hence the relaxation has converged. The default value is \(0.005\:a_{0}\). If units are not defined, then these are thought to be \(a_{0}\). Units “ang” correspond to Å. This criterion can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_disp\_tol: [VALUE]\:[UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_disp\_tol: 0.002\:bohr}\\ & \mathrm{or}\\ & \mathrm{geom\_disp\_tol: 0.001\:ang} \end{aligned}\end{split}\]

Options

Output detail

The output detail of the geometry relaxation process can be controlled by the user. The default behaviour is to follow the \(\mathrm{output\_detail}\) variable that controls the overall output detail of the ONETEP calculation. The available settings for this variable are \(\mathrm{BRIEF}\), \(\mathrm{NORMAL}\), \(\mathrm{VERBOSE}\), \(\mathrm{PROLIX}\), and \(\mathrm{MAXIMUM}\). The level of the output detail relevant to geometry relaxation can be controlled by setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_output\_detail: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_output\_detail: VERBOSE} \end{aligned}\end{split}\]

Continuation

The user can select whether to continue from a previous geometry relaxation or start from scratch. The default value of this logical variable is \(\mathrm{FALSE}\) that means geometry relaxations start from scratch. This option can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_continuation: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_continuation: FALSE} \end{aligned}\end{split}\]

Steps between backups

The user can control the number of geometry optimisation steps between backups of all data for continuation. In other words, this tells the program to write a backup for continuation every \(\mathrm{geom\_backup\_iter}\) steps. The default value of this variable is 1, so ONETEP writes a backup after every step of the geometry relaxation. This value can be increased to save time on writing continuation data. This option can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_backup\_iter: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_backup\_iter: 2} \end{aligned}\end{split}\]

Density Kernel and NGWFs

Steps between reset of density kernel and NGWFs

The user can control the stride with which the density kernel and the Nonorthogonal Generalized Wannier Functions (NGWFs) are being reset. In other words, this tells the program to reset the kernel and NGWFs every \(\mathrm{geom\_reset\_dk\_ngwfs\_iter}\) steps. The default value of this variable is 6, so ONETEP resets these quantities every 6 geometry relaxation steps. Resetting the density kernel and NGWFs every once in a while can prevent problems in converging the energy of the NGWFs during optimisation. This option can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_reset\_dk\_ngwfs\_iter: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_reset\_dk\_ngwfs\_iter: 10} \end{aligned}\end{split}\]

Reuse density kernel and NGWFs

The user can control whether to re-use an existing density kernel and set of NGWFs. The default value of this logical variable is \(\mathrm{TRUE}\) except from the case of a Density-Functional based Tight-Binding (DFTB) calculation, where it is \(\mathrm{FALSE}\) by default. This option can be controlled by the user through setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_reuse\_dk\_ngwfs: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_reuse\_dk\_ngwfs: FALSE} \end{aligned}\end{split}\]

Geometry Relaxation methods

There is a variety of optimisation algorithms implemented in ONETEP. The user can select which algorithm to use by setting the following parameter in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_method: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_method: TPSD} \end{aligned}\end{split}\]

These methods are being discussed in this section.

BFGS

The Broyden-Fletcher-Goldfard-Shanno (BFGS) algorithm is a very popular quasi-Newton optimisation method that is implemented in various computational chemistry codes, including ONETEP. In ONETEP, the BFGS algorithm follows the implementation by Pfrommer et al. [Pfrommer1997]. This method uses an initial Hessian matrix that is updated in an iterative fashion. The domain of this Hessian includes both internal and cell degrees of freedom, hence both nuclear coordinates, \(\mathbf{R}\), and lattice vectors, \(\mathbf{h}\), are relaxed. The following notation is used for the lattice vectors,

(68)\[ \begin{aligned} \mathbf{h}=[UVW]\end{aligned}\]

in more detail, if the unit vectors along the x, y, and z directions in Cartesian space are \(\mathbf{\hat{i}}\), \(\mathbf{\hat{j}}\), and \(\mathbf{\hat{k}}\), respectively, then

(69)\[ \begin{aligned} \mathbf{h} = U\mathbf{\hat{i}} + V\mathbf{\hat{j}} + W\mathbf{\hat{k}}\end{aligned}\]

The BFGS algorithm uses information from both forces and the Hessian matrix to investigate a minimum. The latter is computationally expensive as it is \(O(N^2)\) [Aarons]. The Hessian should be an operator that transforms between the changes in nuclear positions and forces,

(70)\[ \begin{aligned} \mathbf{H}_{n+1}\Delta \mathbf{R}_n=\Delta \mathbf{F}_n\end{aligned}\]

where \(\mathrm{\Delta \mathbf{R}_n}\) and \(\mathrm{\Delta \mathbf{F}_n}\) are the changes in positions and forces between steps \(n-1\) and \(n\), respectively.

Then, the algorithm updates its guess solution based on,

(71)\[ \begin{aligned} \mathbf{H}_{n+1}^{-1}=(\mathbf{I}-\mathbf{A})\mathbf{H}_{n}^{-1}(\mathbf{I}-\mathbf{A})+\mathbf{A}\end{aligned}\]

where,

(72)\[ \begin{aligned} \mathbf{A}=\mathbf{\rho}_{n}\Delta\mathbf{F}_n(\Delta\mathbf{R}_n)^{T}\end{aligned}\]

(73)\[ \begin{aligned} \mathbf{\rho}_{n}=\frac{1}{(\Delta\mathbf{F}_n)^{T}\Delta\mathbf{R}_n}\end{aligned}\]

Therefore, the BFGS algorithm updates the inverse Hessian matrix at every step, as it is more computationally efficient than updating the Hessian and then inverting it at every step. At last, the BFGS algorithm can be selected by setting the \(\mathrm{geom\_method}\) variable to \(\mathrm{BFGS}\) in the ONETEP input file.

Initial Inverse Hessian Matrix

In ONETEP, the initial inverse Hessian matrix is set up as,

(74)\[\begin{split} \begin{aligned} H_{0}^{-1}= \begin{bmatrix} (3\Omega B_{0})^{-1} & 0 & \dots & & & 0 \\ 0 & \ddots & 0 & \dots & & \vdots \\ \vdots & 0 & (3\Omega B_{0})^{-1} & 0 & \dots & \\ & \vdots & 0 & g_{0}^{-1}\langle m_{ionic}^{-1}\rangle\omega_{0}^{-2} & 0 & & \\ &&\vdots & 0 &\ddots&0\\ 0 & \dots & & & 0 & g_{0}^{-1}\langle m_{ionic}^{-1}\rangle\omega_{0}^{-2} \end{bmatrix} \end{aligned}\end{split}\]

(75)\[ \begin{aligned} \Omega = det(\mathbf{h}) \end{aligned}\]

(76)\[ \mathbf{h}=(1+\epsilon)\mathbf{h_{0}}\]

(77)\[ \mathbf{g_{0}}=\mathbf{h_{0}}^{T}\mathbf{h_{0}}\]

where \(\mathrm{B_{0}}\) is the bulk modulus, \(\Omega\) is the cell volume, \(\mathbf{g_{0}}\) is the \(3N \times 3N\) metric tensor of the initial configuration, \(\mathrm{\langle m_{ionic} \rangle}\) is the average ionic mass, \(\mathrm{\omega_{0}^{-2}}\) is the average phonon frequency at the \(\mathrm{\Gamma}\) point, and \(\epsilon\) is the finite strain tensor. This is a block-diagonal matrix. The upper left \((9 \times 9)\) diagonal part describes cell-cell interactions, while the bottom right \((3N \times 3N)\) diagonal part describes ion-ion interactions. This way, we can calculate elastic properties and phonon frequencies at the \(\Gamma\)-Point [Pfrommer1997] [Aarons].

Line Search

So far we have learnt how to calculate the energy, its gradient and its Hessian with respect to nuclear positions. Now we are interested in how to decide where the next point for which these quantities are calculated should be on the PES. In simple terms, we need to find out where we should look after calculating the energy of a point and the local curvature of its region. We identify the search direction, \(p_{n}\), after every geometry relaxation step using the following expression,

(78)\[ \begin{aligned} \mathbf{p}_{n}=-\mathbf{H}_{n}^{-1}\nabla E(\mathbf{R}_{n})\end{aligned}\]

hence the next point is calculated using the search direction and an arbitrarily chosen step length, \(\lambda_{n}\), as follows,

(79)\[ \begin{aligned} \mathbf{R}_{n+1}=\mathbf{R}_{n}+\lambda_{n}\mathbf{p}_{n},\hspace{0.5cm}\lambda_{n}>0\end{aligned}\]

Conditions for step length

The step length, \(\lambda_{n}\), should be determined following Wolfe’s conditions [Wolfe1969] [Wolfe1971]. In ONETEP, weak Wolfe-Powell conditions are used. These are described in detail by Gilbert [Gilbert1997] and Yuan et al. [Yuan2017]. The following conditions should be satisfied for the next step, \(\mathbf{R}_{n+1}\),

(80)\[ \begin{aligned} E(\mathbf{R}_{n+1}) \leq E(\mathbf{R}_{n}) + \omega_{1}\lambda_{n}\nabla E(\mathbf{R}_{n})^{T}\mathbf{p}_{n} \end{aligned}\]

(81)\[ \begin{aligned} \nabla E(\mathbf{R}_{n+1})^{T}\mathbf{p}_{n}\geq \omega_{2}\nabla E(\mathbf{R}_{n})^{T}\mathbf{p}_{n} \end{aligned}\]

(82)\[ \begin{aligned} 0<\omega_{1}<0.5 \end{aligned}\]

(83)\[ \begin{aligned} \omega_{1}<\omega_{2}<1 \end{aligned}\]

where \(\omega_{1}\) and \(\omega_{2}\) are constants independent of the current step. These conditions lead to a descending search direction on the PES [Gilbert1997] [Yuan2017]. They also help with the convergence of the optimisation algorithm [Gilbert1997] [Yuan2017].

Limited-Memory BFGS (L-BFGS)

The limited-memory BFGS (L-BFGS) method can be useful when we have large systems, hence the computational cost of calculating the Hessian matrix is very high. In L-BFGS, the Hessian, that is a \(\mathrm{(3N + 9) \times (3N + 9)}\) matrix, where \(\mathrm{N}\) is the number of atoms in the system, is not stored in full. A set of vectors of length \(\mathrm{N}\) is stored instead, hence the optimisation converges at a linear rate. An approximate Hessian matrix is constructed based on the matrix that was used in the last few steps. This matrix should be sparse, symmetric, and positive-definite [Liu1989]. As in the standard BFGS algorithm, the inverse Hessian matrix is updated at each optimisation step. In L-BFGS, we do not need to store the Hessian but we need to access information about the positions and gradients at previous steps [Packwood2016]. We choose to store a certain number of sets of positions and gradients, namely \(\mathrm{m}\), and every time a new optimisation step is made, the oldest set is removed from storage to make space for the latest set to be stored. The number of sets, \(\mathrm{m}\) is specified by the user. By default, ONETEP uses \(\mathrm{m}\) equal to 30. We declare the difference in positions and gradients between steps \(n-1\) and \(n\) as \(\mathrm{s_{n}}\) and \(\mathrm{y_{n}}\). Then, we have the following expressions [Aarons],

(84)\[\begin{aligned} \mathbf{s}_{n}=\mathbf{R}_{n}-\mathbf{R}_{n-1} \end{aligned}\]

(85)\[\begin{aligned} \mathbf{y}_{n}=\nabla E(\mathbf{R}_{n})-\nabla E(\mathbf{R}_{n-1}) \end{aligned}\]

(86)\[\begin{aligned} \mathbf{\rho}_{n}=\frac{1}{\mathbf{y}_{n}^{T}\mathbf{s}_{n}} \end{aligned}\]

(87)\[\begin{aligned} \mathbf{S}_{n} = \begin{bmatrix} \mathbf{s}_{0},...,\mathbf{s}_{n-1} \end{bmatrix} \end{aligned}\]

(88)\[\begin{aligned} \mathbf{Y}_{n} = \begin{bmatrix} \mathbf{y}_{0},...,\mathbf{y}_{n-1} \end{bmatrix} \end{aligned}\]

An initial approximation of the inverse Hessian matrix, \(H^{-1}_{0}\), is used at the first iteration of the algorithm. In contrast with the standard BFGS, the initial matrix approximation can be different at each step [Liu1989]. The inverse Hessian can be updated using [Byrd1994],

(89)\[\begin{split}\begin{aligned} \mathbf{H}^{-1}_{n}=\mathbf{H}^{-1}_{0}+ \begin{bmatrix} \mathbf{S}_{n} & \mathbf{H}^{-1}_{0}\mathbf{Y}_{n} \end{bmatrix} \mathbf{W}_{n} \begin{bmatrix} \mathbf{S}^{T}_{n}\\ \mathbf{Y}^{T}_{n}\mathbf{H}^{-1}_{0} \end{bmatrix}\\ \end{aligned}\end{split}\]

(90)\[\begin{split}\begin{aligned} \mathbf{W}_{n}=\begin{bmatrix} \mathbf{R}_{n}^{-T}(\mathbf{D}_{n}+\mathbf{Y}^{T}_{n}\mathbf{H}^{-1}_{0}\mathbf{Y}_{n})\mathbf{R}_{n}^{-T} & -\mathbf{R}^{-T}_{n}\\ -\mathbf{R}^{-T}_{n} & 0 \end{bmatrix}\\ \end{aligned}\end{split}\]

(91)\[\begin{split}\begin{aligned} \mathbf{D}_{n} = \begin{bmatrix} \mathbf{s}^{T}_{0}\mathbf{y}_{0} & 0 & \ldots & 0 \\ 0 & \mathbf{s}^{T}_{1}\mathbf{y}_{1} & & \vdots \\ \vdots & & \ddots & 0 \\ 0 & \ldots & 0 & \mathbf{s}^{T}_{n}\mathbf{y}_{n} \end{bmatrix} \end{aligned}\end{split}\]

In BFGS, \(\mathbf{H}^{-1}_{n}\) is multiplied by vector \(\mathbf{v}\) and gives a product vector, \(\mathbf{p}\).

(92)\[ \begin{aligned} \mathbf{p} \rightarrow \mathbf{H}^{-1}_{n}\mathbf{v} \end{aligned}\]

but in L-BFGS we do not compute \(\mathbf{H}^{-1}_{n}\). Consequently, we need to find a way to obtain vector \(\mathbf{p}\). In ONETEP, this is achieved by using the Basic Linear Algebra Subprogram (BLAS) libraries to perform matrix operations in the following fashion as explained in detail in [Aarons],

(93)\[ \begin{aligned} \mathbf{p} = \mathbf{H}_{0}^{-1}\mathbf{v} \end{aligned}\]

(94)\[ \begin{aligned} \mathbf{w}_{1:m}=\mathbf{Y}_{n}^{T}\mathbf{p} \end{aligned}\]

(95)\[ \begin{aligned} \mathbf{w}_{m+1:2m}=\mathbf{S}_{n}^{T}\mathbf{v} \end{aligned}\]

(96)\[ \begin{aligned} \mathbf{w}_{1:m} \rightarrow \mathbf{R}_{n}^{-1}\mathbf{Y}_{n}^{T}\mathbf{H}_{0}^{-1}\mathbf{v} \end{aligned}\]

(97)\[ \begin{aligned} \mathbf{w}_{m+1:2m} \rightarrow \mathbf{R}_{n}^{-1}\mathbf{S}_{n}^{T}\mathbf{v} \end{aligned}\]

(98)\[ \begin{aligned} \mathbf{\Xi} = \mathbf{T}_{n} \end{aligned}\]

(99)\[ \begin{aligned} \mathbf{\Xi} \rightarrow \mathbf{R}_{n}^{-1} \mathbf{\Xi} \end{aligned}\]

(100)\[ \begin{aligned} \mathbf{w}_{1:m} \rightarrow \mathbf{w}_{1:m}- \mathbf{\Xi} \mathbf{w}_{m+1:2m} \end{aligned}\]

(101)\[ \begin{aligned} \mathbf{p} \rightarrow \mathbf{p} + \mathbf{S}_{n}^{T}\mathbf{w}_{1:m} \end{aligned}\]

(102)\[ \begin{aligned} \mathbf{t} = -\mathbf{Y}_{n}^{T}\mathbf{w}_{m+1:2m} \end{aligned}\]

(103)\[ \begin{aligned} \mathbf{p} \rightarrow \mathbf{p} + \mathbf{H}_{0}^{-1}\mathbf{t} \end{aligned}\]

where, \(\mathbf{w}\), \(\mathbf{t}\) are vectors of lengths \(\mathrm{2m}\) and \(\mathrm{n}\), respectively. \(\mathbf{\Xi}\) is a \(\mathrm{m \times m}\) matrix. The L-BFGS algorithm uses this procedure until convergence.

Options

The following variables can be set when the L-BFGS algorithm is selected. The user is advised to follow the default behaviour here. Nevertheless, there is an option to modify these settings as explained in the following text.

• L-BFGS maximum updates

  This variable determines the number of vectors updated in L-BFGS. The default value is 30. This means that 30 vectors will be updated at each iteration. This variable can be controlled by the user through setting the following parameter in the input file,
  \[\begin{split}\begin{aligned} & \mathrm{lbfgs\_max\_updates: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{lbfgs\_max\_updates: 30} \end{aligned}\end{split}\]
• L-BFGS block length

  This variable determines the number of updates that are stored in an unbounded L-BFGS calculation before reallocation. The default value is 30. This means that 30 updates will be stored. This variable can be controlled by the user through setting the following parameter in the input file,
  \[\begin{split}\begin{aligned} & \mathrm{lbfgs\_block\_length: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{lbfgs\_block\_length: 30} \end{aligned}\end{split}\]
• Estimated bulk modulus

  The user can provide an estimate of the bulk modulus. The default value of this variable is 0.017 \(E_{H}\:a_{0}^{-3}\). This is one of the parameters used to initialize the inverse Hessian matrix. This option can be controlled by the user through setting the following parameter in the input file,
  \[\begin{split}\begin{aligned} & \mathrm{geom\_modulus\_est: [VALUE]\: [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_modulus\_est: 0.02\: Ha\:/\:bohr**\:3} \end{aligned}\end{split}\]
• Estimated average phonon frequency

  The user can provide an estimate of the average phonon frequency at the \(\Gamma\)-point. The default value of this variable is 0.0076 \(E_{H}\). This is one of the parameters used to initialize the inverse Hessian matrix. This option can be controlled by the user through setting the following parameter in the input file,
  \[\begin{split}\begin{aligned} & \mathrm{geom\_frequency\_est: [VALUE]\: [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_frequency\_est: 0.008\:Ha}\\ & \mathrm{or}\\ & \mathrm{geom\_frequency\_est: 0.218\:eV} \end{aligned}\end{split}\]
• Print inverse Hessian matrix

  The user can choose whether to print the inverse Hessian matrix. The default value of this variable is \(\mathrm{FALSE}\), so this matrix is not printed unless the user specifies otherwise. This option can be controlled by the user through setting the following parameter in the input file,
  \[\begin{split}\begin{aligned} & \mathrm{geom\_print\_inv\_hessian: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_print\_inv\_hessian: FALSE} \end{aligned}\end{split}\]

Also, certain preconditioners can be used in the L-BFGS algorithm. These are the exponential (EXP) [Packwood2016] and forcefield (FF)-based [Mones2018] preconditioners. It should be noted that no preconditioner is used by default. Preconditioner options are preset to default values, but the user has the option to change these, if needed. These are \(\mathrm{r_{cut}}\), \(\mathrm{r_{NN}}\), \(\mathrm{A}\), \(\mathrm{\mu}\), and they are used in the following expressions to define the preconditioner \(\mathrm{P}\) options. Either can be selected by setting the following variable in the input file,

\[\begin{split}\begin{aligned} & \mathrm{geom\_precond\_type: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_type: EXP} \end{aligned}\end{split}\]

The preconditioners can be modified (if needed) by setting the appropriate variables,

\[\begin{split}\begin{aligned} & \mathrm{geom\_precond\_exp\_c\_stab: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_exp\_c\_stab: 0.1}\\ & \\ & \\ & \mathrm{geom\_precond\_exp\_a: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_exp\_a\_stab: 3.0}\\ & \\ & \\ & \mathrm{geom\_precond\_exp\_r\_nn: [VALUE]\ [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_exp\_r\_nn: 0.1\:bohr}\\ & \\ & \\ & \mathrm{geom\_precond\_exp\_r\_cut: [VALUE] [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_exp\_r\_cut: 0.1\:bohr}\\ & \\ & \\ & \mathrm{geom\_precond\_exp\_mu: [VALUE] [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_exp\_mu: 0.1\: Ha\:/\:bohr**\:2}\\ & \\ & \\ & \mathrm{geom\_precond\_ff\_c\_stab: [VALUE] [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_ff\_c\_stab: 0.1\: Ha\:/\:bohr**\:2}\\ & \\ & \\ & \mathrm{geom\_precond\_ff\_r\_cut: [VALUE] [UNITS]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_precond\_ff\_r\_cut: 3.8\:bohr}\\ \end{aligned}\end{split}\]

At last, the L-BFGS algorithm can be selected by setting the \(\mathrm{geom\_method}\) variable to \(\mathrm{LBFGS}\) in the ONETEP input file.

Coordinate system

The user can choose if Cartesian or internal (delocalised) coordinates will be used during geometry relaxation. The latter are generated based on the implementation by Andzelm et al. [Andzelm2001]. Cartesian coordinates are used in all geometry relaxation methods by default. The user can select which system of coordinates to use by setting the \(\mathrm{geom\_method}\) variable to either \(\mathrm{CARTESIAN}\) or \(\mathrm{DELOCALIZED}\). For the latter, only the BFGS method is used. The use of delocalised coordinates can improve performance of the geometry relaxation. When Cartesian coordinates are selected by setting the \(\mathrm{geom\_method}\) variable in the input file, the user can choose whether to do a \(\mathrm{BFGS}\) or \(\mathrm{L-BFGS}\) optimisation by setting the parameter to \(\mathrm{FALSE}\) or \(\mathrm{TRUE}\), respectively. This is shown below,

\[\begin{split}\begin{aligned} & \mathrm{geom\_lbfgs: [VALUE]}\\ & \mathrm{e.g.,}\\ & \mathrm{geom\_lbfgs: TRUE} \end{aligned}\end{split}\]

Two-point Steepest Descents (TPSD)

The two-point steepest descents (TPSD) optimisation algorithm is implemented in ONETEP. This is based on the work of Barzilai and Borwein [Barzilai1988]. The update equation can be obtained in the same way as in the BFGS algorithm. The search direction, \(p_{n}\), can be calculated as,

(104)\[ \begin{aligned} p_{n}=-\nabla E(\mathbf{R}_{n}) \end{aligned}\]

In this method, we need to calculate the change in atomic positions, \(\Delta\mathbf{R}\), and the gradient of the energy with respect to atomic position, \(\Delta(\nabla E (\mathbf{R}))\), between the current iteration, \(i\), and the previous one, \(i-1\). Please note that in what follows in this section, we will just rename the quantity \(\nabla E (\mathbf{R}_{i})\) to \(\mathbf{g}_{i}\) for simplicity.

(105)\[ \begin{aligned} \Delta\mathbf{R}=\mathbf{R}_{i}-\mathbf{R}_{i-1} \end{aligned}\]

(106)\[ \begin{aligned} \Delta\mathbf{g}=\mathbf{g}_{i}-\mathbf{g}_{i-1} \end{aligned}\]

consequently, the step length, \(\lambda_{n}\), is calculated either as,

(107)\[ \begin{aligned} \lambda_{n}=\frac{\Delta\mathbf{R} \cdot \Delta\mathbf{g}}{\Delta\mathbf{g} \cdot \Delta\mathbf{g}} \end{aligned}\]

this way we minimise the quantity \(\lVert\Delta\mathbf{R}-\lambda\Delta\mathbf{g}\rVert^{2}\) with respect to \(\lambda\). In ONETEP, this equation is used to calculate the step length, \(\lambda_{n}\), by default. Symmetrically, we can use,

(108)\[ \begin{aligned} \lambda_{n}=\frac{\Delta \mathbf{R} \cdot \Delta \mathbf{R}}{\Delta \mathbf{R} \cdot \Delta \mathbf{g}} \end{aligned}\]

to minimise the quantity \(\lVert\lambda\Delta\mathbf{R}-\Delta\mathbf{g}\rVert^{2}\) with respect to \(\lambda\).

At last, the TPSD algorithm can be selected by setting the \(\mathrm{geom\_method}\) variable to \(\mathrm{TPSD}\) in the ONETEP input file.

ASE Optimizers

In addition to the optimisation algorithms implemented in ONETEP, all optimisation algorithms available in the Atomic Simulation Environment (ASE) [ase_optimizers_website] can be used as well. This can be done through the interface between ONETEP and ASE [onetep_ase_interface]. This way, ONETEP works as the calculator that ASE uses to compute the energy and forces of a given system at each step of the relaxation process. Then, the propagation of the geometry relaxation process, i.e., the search direction, step length, and propagation formula, is handled by the optimisation algorithm selected in ASE.

Using the interface between ONETEP and the Atomic Simulation Environment (ASE)

Requirements

Before using the ONETEP / ASE interface, we need to make sure that we have installed python (preferably version 3 as the following code is written using python3 syntax). Then, we should have installed the following python packages: ASE (Atomic Simulation Environment), and OS (Operating System). The OS package lets us execute ONETEP as well as read and write ONETEP files. A couple of important packages that is highly recommended to be installed are NumPy (Numerical Python) and SciPy (Scientific Python). These handle advanced numerical (e.g., linear algebra, powers, etc.) and scientific calculations (e.g., integration, interpolation, etc.), respectively. The ASE package allows for the manipulation of atomic/molecular systems. An interface between ONETEP and ASE is already in place and it lets us call ONETEP from ASE, make calculations in ONETEP, and communicate back with ASE. The advantages of using ASE with ONETEP are numerous. A number of these advantages is given in the following list,

• Optimisers built in ASE can be used to drive geometry relaxation in addition to the ones available in ONETEP.

• Molecular systems can be manipulated, e.g., translated and rotated inside the unit cell.

• Various python packages focused on molecular systems can be used in conjunction with the ASE/ONETEP interface. For example, packages for global optimisation can be used to find the global minimum on the PES.

• We can easily convert between popular molecular input/output files. For example, we can convert a .cif file that contains crystallographic data to an .xyz atomic coordinate file that can be used in ONETEP.

• ASE can be used as a standalone visualisation package. For example, it can be used to visualise a trajectory of atomic positions.

The aforementioned packages can be installed using

python3 -m pip install package_name

where one should replace package_name with the name of the package to be installed. For example,

python3 -m pip install ase

In our case the names of the packages are,

• os

• ase

and optionally,

• numpy

• scipy

ONETEP / ASE interface using intrinsic optimisation algorithms

In this example, we see how to use the ONETEP / ASE interface while opting for an optimisation algorithm that is already implemented in ONETEP. The following code can be written (saved) to a file called \(\mathrm{input\_intrinsic\_algorithm.py}\). Then, we could run our ONETEP calculation by just running this python script as follows,

python3 input_intrinsic_algorithm.py > output_intrinsic_algorithm.log

where we redirect the output to a file called \(\mathrm{output\_intrinsic\_algorithm.log}\).

This way, ASE creates an input file for ONETEP, then ONETEP performs the geometry relaxation, and it communicates the energy and forces back to ASE for post-processing and visualisation.

from os import environ, path
from ase.build import molecule
from ase.calculators.onetep import Onetep
from ase.io import read,iread,write

# set ONETEP run command by providing the full
# path to the ONETEP executable. Here we also
# set the number of MPI ranks and threads per rank
# based on what resources we have asked for.
environ["ASE_ONETEP_COMMAND"]="export OMP_NUM_THREADS=$SLURM_THREADS_PER_CORE; srun -n $SLURM_NPROCS /path/to/onetep/bin/onetep PREFIX.dat >> PREFIX.out 2> PREFIX.err"

# read atomic positions from an .xyz file
# that is in the same directory.
mol = read('./mymolecule.xyz')

# set lattice vectors (in Angstrom)
# replace xx, xy, xz, yx, yy, yz,
# zx, zy, zz with desired values
# for the lattice vectors
mol.set_cell([[xx,xy,xz],
              [yx,yy,yz],
              [zx,zy,zz]])

# set calculator as Onetep and a
# label for input and output files.
calc_label = 'mylabel'
calc = Onetep(label=calc_label)

# set Onetep parameters (left-hand side) and
# corresponding values (right-hand side).
# change atom name "A" and any other
# value you want in the code below.
calc.set(pseudo_path='/path/to/pseudo/',
         pseudo_suffix='.recpot',
         task='GeometryOptimization',
         geom_method='TPSD',
         geom_force_tol='0.05 "ev/ang"',
         write_forces=True,
         write_xyz=True,
         xc='PBE',
         cutoff_energy='1200 eV',
         species_ngwf_number={"A":10},
         species_ngwf_radius={"A":12.0}, # [bohr]
         write_hamiltonian=True,
         write_tightbox_ngwfs=True,
         write_denskern=True,
         output_detail='verbose',
         )

# perform the calculation
mol.calc = calc

# get atomic positions, energy, and forces from the
# calculator. In our case, the calculator is ONETEP.
mol.get_positions()
mol.get_forces()
mol.get_potential_energy()

ONETEP / ASE interface using ASE optimisation algorithms

In this example, we see how to use the ONETEP / ASE interface while opting for an optimisation algorithm that is implemented in ASE. The following code can be written (saved) to a file called \(\mathrm{input\_ase\_algorithm.py}\). Then we could run our ONETEP calculation by just running this python script as follows,

python3 input_ase_algorithm.py > output_ase_algorithm.log

where we redirect any output to a file called \(\mathrm{output\_ase\_algorithm.log}\).

This way, ASE creates an input file for ONETEP, then ONETEP calculates the energy and forces, and it communicates the energy and forces back to ASE, then ASE updates the structure until the desired convergence threshold has been reached. Final structures, energy, and forces are available in ASE for post-processing and visualisation.

from os import environ, path
from ase.build import molecule
from ase.calculators.onetep import Onetep
from ase.optimize.sciopt import SciPyFminBFGS
from ase.io import read,iread,write

# set ONETEP run command by providing the full
# path to the ONETEP executable. Here we also
# set the number of MPI ranks and threads per rank.
# based on what resources we have asked for.
environ["ASE_ONETEP_COMMAND"]="export OMP_NUM_THREADS=$SLURM_THREADS_PER_CORE; srun -n $SLURM_NPROCS /path/to/onetep/bin/onetep PREFIX.dat >> PREFIX.out 2> PREFIX.err"

# read atomic positions from an .xyz file
# that is in the same directory.
mol = read('./mymolecule.xyz')

# set lattice vectors (in Angstrom)
# replace xx, xy, xz, yx, yy, yz,
# zx, zy, zz with desired values
# for the lattice vectors.
# For orthogonal cells, you can set the cell as
# mol.set_cell([xx,yy,zz])
mol.set_cell([[xx,xy,xz],
              [yx,yy,yz],
              [zx,zy,zz]])

# set calculator as Onetep and a
# label for input and output files.
calc_label = 'mylabel'
calc = Onetep(label=calc_label)

# set ONETEP parameters (left-hand side) and
# corresponding values (right-hand side).
# change atom name "A" and any other
# value you want in the code below.
calc.set(pseudo_path='/path/to/pseudo/potential/',
         pseudo_suffix='.recpot',
         task='SinglePoint',
         xc='PBE',
         cutoff_energy='1200 eV',
         species_ngwf_number={"A": 10},
         species_ngwf_radius={"A": 12.0}, # [bohr]
         write_hamiltonian=True,
         write_tightbox_ngwfs=True,
         write_denskern=True,
         output_detail='verbose',
         )

# these files need to be read to
# update the relaxation process.
if path.isfile(calc_label + '.dkn') == True:
   calc.set(read_denskern=True)
if path.isfile(calc_label + '.ham') == True:
   calc.set(read_hamiltonian=True)
if path.isfile(calc_label + '.tightbox_ngwfs') == True:
   calc.set(read_tightbox_ngwfs=True)

# perform the calculation
mol.calc = calc

# get energy and forces from the calculator
# in our case, the calculator is ONETEP.
mol.get_forces()
mol.get_potential_energy()

# select optimisation algorithm and relevant options.
# Here, we select the SciPyFminBFGS algorithm and
# we write the trajectory to a .traj file.
opt = SciPyFminBFGS(mol, trajectory='opt.traj')

# optimise structure until the maximum force on any
# atom is equal or less than 0.05 (units are eV/A).
opt.run(fmax=0.05)

# convert ASE trajectory (.traj) to .xyz format
trj = iread("opt.traj")
trj_xyz = write("opt_traj.xyz", trj, format="xyz")

Tutorials

In this section, a series of tutorials is demonstrated. Please create a separate folder (directory in Unix-based systems, such as Linux distributions) for each one of the tutorials, and put all files of each tutorial in the corresponding folder. We will learn how to create a guess geometry for a certain system, e.g., a set of atoms, a molecule, a molecular cluster, and then relax it using ONETEP. These examples include an ethanol molecule and a platinum nanoparticle. We note that the focus of these tutorials is to learn how to use optimisation algorithms in ONETEP, and these can be applied to much more complicated systems following the same rationale as in these tutorials.

Ethanol

At first, we are going to relax the geometry of a simple organic molecule that is ethanol (\(C_{2}H_{5}OH\)). A guess geometry can be provided either directly in the ONETEP input file or through an XYZ file that can be loaded in ONETEP. Please create a folder named however you prefer, e.g., \(\mathrm{ethanol\_example}\) and put all files in that folder. In this example, we are going to use the Avogadro software [Avogadro] [Hanwell2012] to create an ethanol molecule. In Avogadro, select the pencil icon from the toolbar at the top. Then, select Carbon from the “Draw” toolbar by clicking on the box right next to “Element” on the left hand side. Click and drag somewhere on the black canvas so that a C-C single bond is created and Avogadro will automatically adjust hydrogen atoms to make it a \(CH_{3}CH_{3}\) molecule. Select Oxygen in the same way as carbon was previously selected. Click on a carbon atom on the black canvas and drag to make a C-O bond (again, hydrogen atoms will be adjusted automatically). Use the auto-optimize tool that is on the same toolbar as the pencil icon (it has an E sign and a down-pointing arrow below E). This will do a rough relaxation to provide a reasonable initial guess geometry. At last, click on “File” that is the left-most option on the top toolbar and click either on “save as” or hover the mouse over export and then click on “molecule”. A new window will appear, where the coordinates can be saved in an XYZ file. Click on “All files” at the bottom right and select “XYZ”, then select a name for the file while including the .xyz extension (for example, \(\mathrm{ethanol.xyz}\)). Exit Avogadro and move this XYZ file to the directory where the ONETEP simulation will be performed. The XYZ format is a readable text file which can be viewed and modified with any text editor. This contains the Cartesian coordinates of all the atoms in the system. An example \(\mathrm{ethanol.xyz}\) is provided below,

9
XYZ file generated by Avogadro.
C     -4.63004     0.41911    0.07151
C     -3.76666     1.67624    0.06260
H     -4.34884    -0.23171    0.89807
O     -2.40610     1.40089   -0.17922
H     -2.09824     0.76731    0.47816
H     -5.67688     0.68678    0.18150
H     -4.50180    -0.12684   -0.85976
H     -4.07361     2.34155   -0.74747
H     -3.88245     2.21413    1.01544

Now that we have our molecule, we will relax its geometry in ONETEP.

ONETEP built-in optimizer

First, we are going to use optimisation algorithms which are built-in ONETEP. In this example, we choose the two-point steepest descent, \(\mathrm{TPSD}\), algorithm. An ONETEP input file should have at least the following sections,

• general parameters

• lattice vectors block

• species block

• potential block

• positions block

• etc.

An example input script, \(\mathrm{ethanol\_geo\_opt.dat}\), is provided below,

# ethanol_geo_opt.dat
# general parameters
# kinetic energy cutoff
cutoff_energy : 1000 eV
# density kernel cutoff
kernel_cutoff : 1000 bohr
# level of detail of the output
output_detail : verbose
# task to be performed
task : GeometryOptimization
# optimization algorithm
geom_method: TPSD
# tolerance for the forces to
# evaluate convergence
geom_force_tol: 0.05 "ev/ang"
# print relevant information
write_denskern : True
write_forces : True
write_hamiltonian : True
write_tightbox_ngwfs : True
write_xyz: True
# Exchange-Correlation functional
xc_functional : PBE

# lattice vectors block
# values are in angstrom (using ang keyword)
%BLOCK LATTICE_CART
ang
    15.000000000 0.0000000000 0.0000000000
    0.0000000000 15.000000000 0.0000000000
    0.0000000000 0.0000000000 15.000000000
%ENDBLOCK LATTICE_CART

# species block
# species, name, atomic number,
# number of NGWFs, NGWF radii (in bohr)
%BLOCK SPECIES
    C C 6 4 12.000000
    O O 8 4 12.000000
    H H 1 1 12.000000
%ENDBLOCK SPECIES

# potentials block
# species, file where the potential can be found.
# It is recommended to copy pseudopotential files to
# the directory, where we perform the calculation.
%BLOCK SPECIES_POT
    C "C.recpot"
    H "H.recpot"
    O "O.recpot"
%ENDBLOCK SPECIES_POT

# positions in Angstrom
%BLOCK POSITIONS_ABS
ang
C -4.63004  0.41911  0.07151
C -3.76666  1.67624  0.06260
H -4.34884 -0.23171  0.89807
O -2.40610  1.40089 -0.17922
H -2.09824  0.76731  0.47816
H -5.67688  0.68678  0.18150
H -4.50180 -0.12684 -0.85976
H -4.07361  2.34155 -0.74747
H -3.88245  2.21413  1.01544
%ENDBLOCK POSITIONS_ABS

Lines starting with \(\#\) are comments so they are not read during runtime and they are helpful to explain code functionality. Before proceeding, let’s copy the required pseudopotential files to the current directory by providing the /full/path/to/onetep while using,

\[\begin{split}\begin{aligned} \mathrm{cp\ /full/path/to/onetep/pseudo/carbon.recpot\ C.recpot}\\ \mathrm{cp\ /full/path/to/onetep/pseudo/hydrogen.recpot\ H.recpot}\\ \mathrm{cp\ /full/path/to/onetep/pseudo/oxygen.recpot\ O.recpot} \end{aligned}\end{split}\]

Please change \(\mathrm{/full/path/to/onetep/}\) to the directory where you installed ONETEP. Inside this directory, the ONETEP source code (\(\mathrm{src}\)), documentation (\(\mathrm{doc}\)), binaries (\(\mathrm{bin}\)), etc. are located. It will usually be something like \(\mathrm{/home/user/software/onetep}\), where \(\mathrm{user}\) is your username. We can use an example submission script to perform this optimisation on a high performance computing (HPC) cluster. An important line that needs to be modified in this script is the full path to the ONETEP top directory as before.

#!/bin/bash -l
#SBATCH  -J ethanol   # Job name on the scheduler.
#SBATCH  -p batch     # Queue (partition) type.
#SBATCH  -N 1         # Number of nodes.
#SBATCH  -n 4         # Total number of MPI ranks.
#SBATCH --mem=16G     # Max memory per node.
#SBATCH  -t 01:10:00  # Wallclock time in [hh:mm:ss].

# load modules
# Change the line below the comments to match your
# preferred compiler, mpi, mkl versions.
module load intel-compilers intel-mpi intel-mkl

# on Iridis5 you can use the following modules,
# module load intel-compilers/2021.2.0 intel-mkl/2021.2.0 \
#             intel-mpi/2021.2.0 python/3.9.7

# on ARCHER2 you can use the following modules,
# module load PrgEnv-cray/8.1.0 cce/12.0.3 cray-fftw/3.3.8.11 \
              cray-mpich/8.1.4 cray-python/3.9.7.1

# sim ID.
# Please put a name of your preference to distinguish
# this simulation. This should be the same as the
# ONETEP input file without the .dat extension.
rootname='ethanol_geo_opt'

# Number of threads per MPI rank.
# This value can be modified, even though ONETEP
# works well with 4 threads per rank for most systems.
export OMP_NUM_THREADS=4

# ONETEP top directory full path,
# e.g., "/home/user/software/onetep".
# Need to modify this.
onetep_top="/full/path/to/onetep/"

# Relative location of the ONETEP executable file.
# e.g., ${onetep_top}/bin/onetep.x86_64_gfortran
# Need to modify the name of the executable.
onetep_exe="${onetep_top}/bin/onetep.executable"

# ONETEP launcher. No need to change this.
onetep_launcher="${onetep_top}/utils/onetep_launcher"

# Show shared libraries. No need to change this.
ldd $onetep_exe >\$ldd

# If running on Iridis5, set I_MPI_PMI_LIBRARY
# environmental variable by removing the comment
# sign '#' at the start of the next couple of lines.
#export I_MPI_PMI_LIBRARY\
#=/local/software/slurm/default/lib/libpmi.so

# If running on ARCHER2, export the python-related
# paths. The PYTHONUSERBASE path is an example, hence
# it should be modified to your needs as explained in
# the python section of the ARCHER2 documentation.
# You should copy the correct project code, e.g., t01,
# your username on ARCHER2, and change python3.9 to
# your version of python. You can export these paths
# by removing the comment sign '#' at the start of
# the next four lines.
#export PYTHONUSERBASE=/work/project_code/project_code/username/.local
#export PATH=$PYTHONUSERBASE/bin:$PATH
#export PYTHONPATH\
#=$PYTHONUSERBASE/lib/python3.9/site-packages:$PYTHONPATH

# Command to run ONETEP. No need to change this.
srun \
     -N $SLURM_JOB_NUM_NODES \
     -n $SLURM_NPROCS \
     -e $onetep_exe \
     -t $OMP_NUM_THREADS \
     $onetep_launcher \
     ${rootname}.dat \
     >${rootname}.out \
     2>${rootname}.err

Note that if your run this on a local computer (not on a computing cluster), e.g., your personal desktop or laptop, then you’ll need to remove the lines starting with \(\mathrm{\#SBATCH}\) and replace srun with mpirun, if you have installed the Intel(R) MPI Library on your computer, so your script will become,

#!/bin/bash -l

# sim ID.
# Please put a name of your preference to distinguish
# this simulation. This should be the same as the
# ONETEP input file without the .dat extension.
rootname='ethanol_geo_opt'

# Number of threads per MPI rank.
# This value can be modified, even though ONETEP
# works well with 4 threads per rank for most systems.
export OMP_NUM_THREADS=4

# ONETEP top directory full path.
# e.g., /home/user/software/onetep
# Need to modify this.
onetep_top="/full/path/to/onetep/top/directory"

# Relative location of the ONETEP executable file.
# e.g., ${onetep_top}/bin/onetep.x86_64_gfortran
# Need to modify the name of the executable.
onetep_exe="${onetep_top}/bin/onetep.executable"

# ONETEP launcher. No need to change this.
onetep_launcher="${onetep_top}/utils/onetep_launcher"

# Show shared libraries. No need to change this.
ldd $onetep_exe >\$ldd

# If running on Iridis5, set I_MPI_PMI_LIBRARY
# environmental variable by removing the comment
# sign '#' at the start of the next couple of lines.
#export I_MPI_PMI_LIBRARY\
#=/local/software/slurm/default/lib/libpmi.so

# Command to run ONETEP. No need to change this.
mpirun \
     -np 4 \
     -e $onetep_exe \
     -t $OMP_NUM_THREADS \
     $onetep_launcher \
     ${rootname}.dat \
     >${rootname}.out \
     2>${rootname}.err

In the example submission script, \(\mathrm{submission\_script.sb}\), we request 1 node, 4 MPI ranks in total, 4 OpenMP threads per MPI rank, 16 GB of memory, and 1 hour and 10 minutes to run our simulation using the \(\mathrm{batch}\) queue, and we can distinguish our simulation on the scheduler as it is named as \(\mathrm{ethanol}\). Please note that the number of MPI ranks should be equal or less than the number of atoms in the system. Consequently, for the ethanol molecule we can ask for up to 9 MPI ranks.

(109)\[ \begin{aligned} \mathrm{Number\ of\ MPI\ ranks} \le \mathrm{Number\ of\ atoms\ in\ the\ system} \end{aligned}\]

Here we chose, slightly less than half that number. The total number of cores, \(N_{cores}\), we asked for can be calculated as follows,

(110)\[\begin{aligned} N_{cores}=N_{ranks}\times N_{threads} \end{aligned}\]

(111)\[\begin{aligned} N_{ranks}=N_{nodes}\times N_{ranks\_per\_node} \end{aligned}\]

where \(N_{nodes}\), \(N_{ranks}\), \(N_{ranks\_per\_node}\), \(N_{threads}\), are the number of nodes, the total number of MPI ranks, the number of MPI ranks per node, and threads per MPI rank, respectively. Consequently, in this example we asked for 16 cores (4 MPI ranks in total \(\times\) 4 threads per rank). We submit our script to the scheduler as a batch job using,

\[\mathrm{sbatch\ submission\_script.sb}\]

or we run it on a local computer using a couple of shell commands, the first one gives us permission to execute the script, and the second one actually runs the script

\[\begin{split}\mathrm{chmod\ +x\ submission\_script.sh}\\ \mathrm{sh\ submission\_script.sh}\end{split}\]

We can check if our script is running by looking at the queue. In SLURM, we can use the following command,

\[\mathrm{squeue\ -u\ \$USER}\]

An example output of the command is

\[\begin{split}\begin{aligned} \mathrm{JOBID} & & \mathrm{PARTITION} & & \mathrm{NAME} & & \mathrm{USER} & & \mathrm{ST} & & \mathrm{TIME} & & \mathrm{NODES} & & \mathrm{NODELIST}\\ \mathrm{1915382} & & \mathrm{batch} & & \mathrm{ethanol} & & \mathrm{user} & & \mathrm{R} & & \mathrm{10:25} & & \mathrm{1} & & \mathrm{red465} \end{aligned}\end{split}\]

This tells us that the job has been assigned an identification number that is \(\mathrm{1915382}\), it uses the \(\mathrm{batch}\) partition, its name is \(\mathrm{ethanol}\), it is run by a user named: \(\mathrm{user}\), its current status is: \(\mathrm{R: Running}\), 10 minutes and 25 seconds have elapsed since starting running the script, it is running on 1 node, and the name of this node is \(\mathrm{red465}\). When the script completes its run, nothing will appear under the header above, as no script will be waiting/running in the queue. Please note that if the status is \(\mathrm{PD}\), this means that the start of this script is pending, hence the script is waiting in the queue. ONETEP generates certain files at runtime based on the type of calculation. In our case, the following files were generated,

• ethanol_geo_opt.out - The calculation output.

• ethanol_geo_opt.err - Any errors occured during the calculation. If this is empty then no errors occured. Otherwise, another file called \(\mathrm{ethanol\_geo\_opt.error\_message}\) will be generated, where more information about the error(s) can be found.

• ethanol_geo_opt.tightbox_ngwfs - Information about the NGWFs generated during the calculation.

• ethanol_geo_opt.continuation - Information about restarting a geometry relaxation.

• ethanol_geo_opt.dkn - Information about the density kernel generated during the calculation.

• ethanol_geo_opt.ham - Information about the Hamiltonian used during the calculation.

• ethanol_geo_opt.geom - Trajectory of geometries, energies, and forces during relaxation.

• ethanol_geo_opt.xyz - Trajectory of geometries during relaxation in the XYZ format. This can be used/visualised with many computational chemistry codes, and molecular visualising software.

• ethanol_geo_opt.bib - References that need to be cited for this calculation written using BIB formatting.

We open the output file and we should find a line that reads,

\[\begin{split}\begin{aligned} \mathrm{Finished\ geometry\ optimization\ after\ 5\ iteration(s).}\\ \mathrm{Total\ Energy\ -3.110106446448E+001\ Eh} \end{aligned}\end{split}\]

Consequently, the geometry relaxation made 5 steps and the final total energy of the system is \(\mathrm{-31.10106446448\ Eh}\). This number may be slightly different when you run this example on your computer or a computing cluster due to differences in machine precision and number rounding patterns. The outcome of a geometry relaxation is a more stable configuration of the atoms of the system. Consequently, we should visualize the relaxed geometry. We can do that by opening the \(\mathrm{ethanol\_geo\_opt.xyz}\) file in a molecular visualisation software. We can use Avogadro, or any other software that is able to visualise molecules, to do this. There we can see that distances and angles between the atoms have changed as they have moved to equilibrium positions in which this molecular configuration is more stable. The optimised structure is shown in Fig. 8.

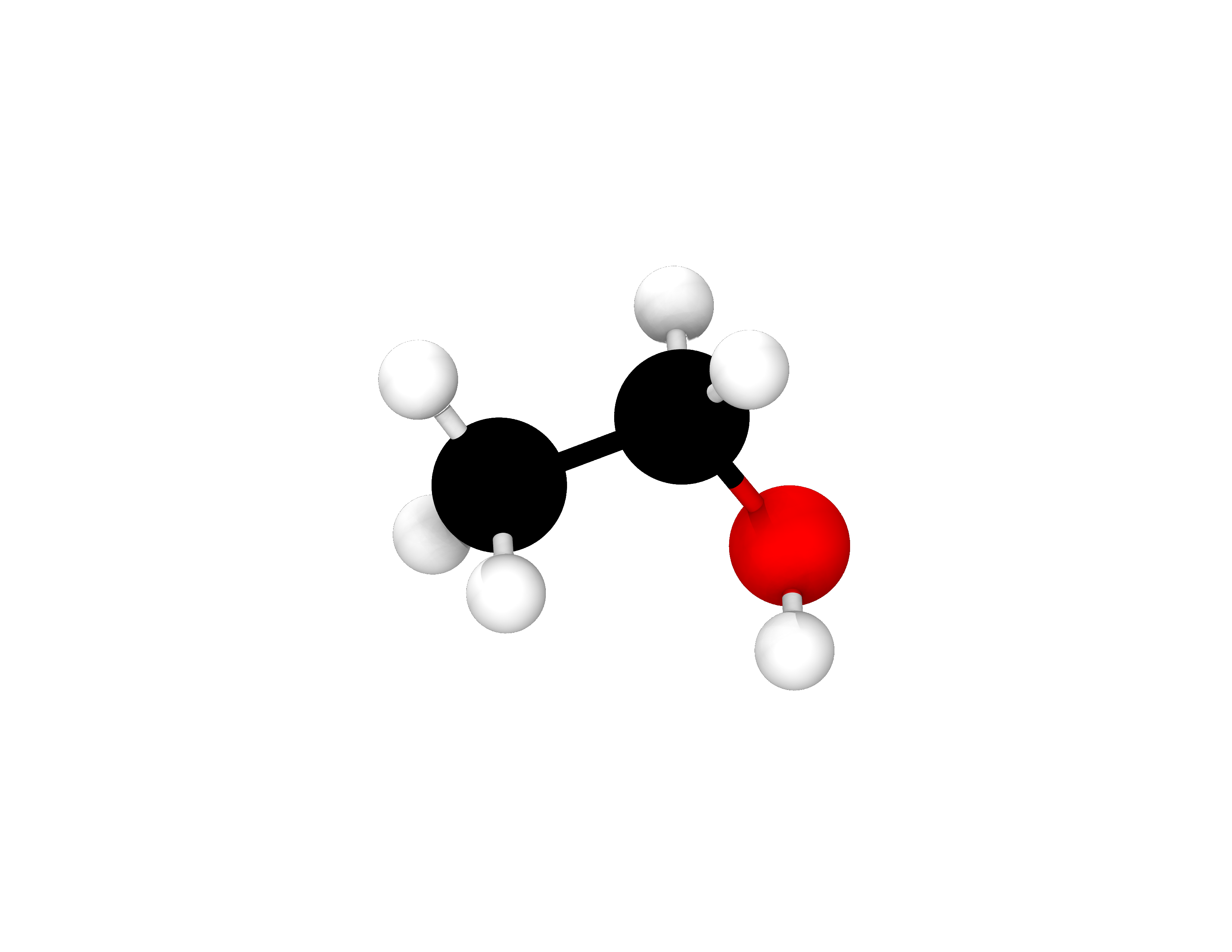
Fig. 8 Atomic configuration of the ethanol molecule after relaxing its geometry in ONETEP. Colour code: carbon - black, oxygen - red, hydrogen - white.

ONETEP built-in optimizer in ASE

The same calculation can be prepared using ASE. Please create a folder named however you prefer, e.g., \(\mathrm{ethanol\_example\_ase}\) and put all files in that folder. We will gather information about the system and calculation parameters in one python file and ASE will generate an ONETEP input file for us. Also, you will see how we can translate the atomic coordinates in ASE, center the molecule in the unit cell, and how ASE can automatically set lattice vectors for us. We follow the guidance provided in Section 5.2 to create an input file in ASE. This should look like the following for the ethanol example,

# ethanol_geo_opt_ase.py
from os import environ, path
from ase.build import molecule
from ase.calculators.onetep import Onetep
from ase.io import read,iread,write

# set ONETEP run command by providing the full
# path to the ONETEP executable. Here we also
# set the number of MPI ranks and threads per rank.
environ["ASE_ONETEP_COMMAND"]="srun -n $SLURM_NPROCS /path/to/onetep/bin/onetep  PREFIX.dat >> PREFIX.out 2> PREFIX.err"

# read atomic positions from an XYZ file
mol=read('ethanol.xyz')

# center the molecule in unit cell. This
# will automatically set the unit cell,
# hence, the lattice vectors provided to ONETEP.
mol.center(vacuum=7.)

# set calculator as Onetep and a
# label for input and output files.
calc_label='ethanol_geo_opt'
calc = Onetep(label=calc_label)

# set Onetep parameters (left-hand side) and
# corresponding values (right-hand side).
calc.set(pseudo_path='./',
         pseudo_suffix='.recpot',
         task='GeometryOptimization',
         geom_method='TPSD',
         geom_force_tol='0.05 "ev/ang"',
         xc='PBE',
         cutoff_energy='1000 eV',
         kernel_cutoff='1000 bohr',
         species_ngwf_number={
            "C":4,"H":1,"O":4},
         species_ngwf_radius={
            "C":12.0,"H":12.0,"O":12.0}, # bohr
         write_denskern=True,
         write_forces=True,
         write_hamiltonian=True,
         write_tightbox_ngwfs=True,
         write_xyz=True,
         output_detail='verbose',
         )

# perform the calculation
mol.calc = calc

# get atomic positions, energy and forces from the
# calculator. In our case, the calculator is ONETEP.
mol.get_positions()
mol.get_potential_energy()

We can use an example submission script to perform this optimisation by running ONETEP through ASE.

#!/bin/bash -l
#SBATCH  -J ethanol   # Job name on the scheduler.
#SBATCH  -p batch     # Queue (partition) type.
#SBATCH  -N 1         # Number of nodes.
#SBATCH  -n 4         # Total number of MPI ranks.
#SBATCH --mem=16G     # Max memory per node.
#SBATCH  -t 01:10:00  # Wallclock time in [hh:mm:ss].

# load modules
# Change the line below the comments to match your
# preferred compiler, mpi, mkl, python versions.
module load intel-compilers intel-mpi intel-mkl python

# on Iridis5 you can use the following modules,
# module load intel-compilers/2021.2.0 intel-mkl/2021.2.0 \
#             intel-mpi/2021.2.0 python/3.9.7

# on ARCHER2 you can use the following modules,
# module load PrgEnv-cray/8.1.0 cce/12.0.3 cray-fftw/3.3.8.11 \
              cray-mpich/8.1.4 cray-python/3.9.7.1

# Number of threads per MPI rank.
# This value can be modified, even though ONETEP
# works well with 4 threads per rank for most systems.
export OMP_NUM_THREADS=4

# If running on Iridis5, set I_MPI_PMI_LIBRARY
# environmental variable by removing the comment
# sign '#' at the start of the next couple of lines.
#export I_MPI_PMI_LIBRARY\
#=/local/software/slurm/default/lib/libpmi.so

# If running on ARCHER2, export the python-related
# paths. The PYTHONUSERBASE path is an example, hence
# it should be modified to your needs as explained in
# the python section of the ARCHER2 documentation.
# Please remember to change the project_code, e.g., t01,
# and the username on ARCHER2. Also, please update
# the python version below to the one you are using.
# You can export these paths by removing the comment
# sign '#' at the start of the next four lines.
#export PYTHONUSERBASE=/work/project_code/project_code/username/.local
#export PATH=$PYTHONUSERBASE/bin:$PATH
#export PYTHONPATH\
#=$PYTHONUSERBASE/lib/python3.9/site-packages:$PYTHONPATH

# run ONETEP through python-ASE
python3 ethanol_geo_opt_ase.py > ethanol_geo_opt_ase_out.log

If running the script on a local computer, remove the lines starting with \(\mathrm{\#SBATCH}\), and follow the same procedure as in the previous example to run the script on your local computer. After running this example, an additional output file is generated. This file is named as \(\mathrm{ethanol\_geo\_opt\_ase\_out.log}\) and it contains the output from the python interface between ASE and ONETEP. This is an empty file. This is due to the fact that calculations were performed only in ONETEP and not in ASE. Calculation output can be found in \(\mathrm{ethanol\_geo\_opt.out}\) once again. As in the previous example, we can visualise the atomic configuration by opening the XYZ file with a software that is able to visualise molecules, such as Avogadro.

Platinum nanoparticle

ASE built-in optimizer

Now we move to a more advanced example where we can relax the geometry of a platinum nanoparticle, \(\mathrm{Pt_{13}}\). Please create a folder named however you prefer, e.g., \(\mathrm{platinum\_example}\) and put all files in that folder. In this example, we will generate the nanoparticle consisting of 13 Pt atoms in ASE and then use an ASE built-in optimisation algorithm to relax its geometry. More information about how to generate nanoparticles in ASE can be found in the ASE manual [ASE_nanoparticle]. In this example, we will use a pseudopotential that was generated on the fly using the CASTEP code [CASTEP] [Pickard2006].

# generate_pt13_ase.py
from ase.cluster import Icosahedron
from ase.io import write

# create a Pt nanoparticle with 2 shells
mol = Icosahedron('Pt', 2)
# save coordinates to an XYZ file
write('pt13.xyz',mol)

Now we will load our geometry saved in an XYZ file in the script that is designed to relax the geometry. We shall place the molecule at the center of the unit cell and add vacuum in three dimensions so that the atoms and corresponding NGWFs are all inside the unit cell.

# pt13_geo_opt_ase.py
from os import environ, path
from ase.build import molecule
from ase.calculators.onetep import Onetep
from ase.io import read,iread,write
from ase.optimize.sciopt import SciPyFminBFGS

# set ONETEP run command by providing the full
# path to the ONETEP executable. Here we also
# set the number of MPI ranks and threads per rank.
environ["ASE_ONETEP_COMMAND"]="srun -n $SLURM_NPROCS /path/to/onetep/bin/onetep PREFIX.dat >> PREFIX.out 2> PREFIX.err"

# load the molecule from an XYZ file
mol = read('pt13.xyz')

# Build unit cell by placing the molecule
# at the centre and add vacuum in three
# dimensions (value in Angstrom).
mol.center(vacuum=7.)

# set calculator as Onetep and a
# label for input and output files.
calc_label = 'pt13_geo_opt'
calc = Onetep(label=calc_label)

# set Onetep parameters (left-hand side) and
# corresponding values (right-hand side).
calc.set(pseudo_path='./',
         pseudo_suffix='_NCP19_PBE_OTF.usp',
         task='SinglePoint',
         xc='PBE',
         cutoff_energy='1000 eV',
         kernel_cutoff='1000 bohr',
         species_ngwf_number={
            "Pt":13},
         species_ngwf_radius={
            "Pt":12.0}, # bohr
         edft=True,
         edft_update_scheme='pulay_mix',
         edft_maxit=10,
         edft_smearing_width='1000 K',
         write_denskern=True,
         write_forces=True,
         write_hamiltonian=True,
         write_tightbox_ngwfs=True,
         write_xyz=True,
         output_detail='verbose',
         )

if path.isfile(calc_label + '.dkn') == True:
   calc.set(read_denskern=True)
if path.isfile(calc_label + '.ham') == True:
   calc.set(read_hamiltonian=True)
if path.isfile(calc_label + '.tightbox_ngwfs') == True:
   calc.set(read_tightbox_ngwfs=True)

# perform the calculation
mol.calc = calc

# get atomic positions, energy and forces from the
# calculator. In our case, the calculator is ONETEP.
mol.get_positions()
mol.get_forces()
mol.get_potential_energy()

# set the optimisation algorithm to ASE built-in
# SciPyFminBFGS and save trajectory in a file.
opt = SciPyFminBFGS(mol, trajectory='opt.traj')
# perform the local optimisation until the maximum
# magnitude of the net force on any atom is 0.05 eV A^(-1).
opt.run(fmax=0.05)

# convert trajectory to the XYZ format
trj = iread("opt.traj")
trj_xyz = write("opt_traj.xyz", trj, format="xyz")

We can slightly modify \(\mathrm{submission\_script\_ase.sb}\) to run this example. The modified submission script follows,

#!/bin/bash -l
#SBATCH  -J pt13      # Job name on the scheduler.
#SBATCH  -p batch     # Queue (partition) type.
#SBATCH  -N 1         # Number of nodes.
#SBATCH  -n 4         # Total number of MPI ranks.
#SBATCH --mem=16G     # Max memory per node.
#SBATCH  -t 01:10:00  # Wallclock time in [hh:mm:ss].

# load modules
# Change the line below the comments to match your
# preferred compiler, mpi, mkl, python versions.
module load intel-compilers intel-mpi intel-mkl python

# on Iridis5 you can use the following modules,
# module load intel-compilers/2021.2.0 intel-mkl/2021.2.0 \
#             intel-mpi/2021.2.0 python/3.9.7

# on ARCHER2 you can use the following modules,
# module load PrgEnv-cray/8.1.0 cce/12.0.3 cray-fftw/3.3.8.11 \
#             cray-mpich/8.1.4 cray-python/3.9.7.1

# Number of threads per MPI rank.
# This value can be modified, even though ONETEP
# works well with 4 threads per rank for most systems.
export OMP_NUM_THREADS=4

# If running on Iridis5, set I_MPI_PMI_LIBRARY
# environmental variable by removing the comment
# sign '#' at the start of the next couple of lines.
#export I_MPI_PMI_LIBRARY\
#=/local/software/slurm/default/lib/libpmi.so

# If running on ARCHER2, export the python-related
# paths. The PYTHONUSERBASE path is an example, hence
# it should be modified to your needs as explained in
# the python section of the ARCHER2 documentation.
# You should copy the correct project code, e.g., t01,
# your username on ARCHER2, and change python3.9 to
# your version of python. You can export these paths
# by removing the comment sign '#' at the start of
# the next four lines.
#export PYTHONUSERBASE=/work/project_code/project_code/username/.local
#export PATH=$PYTHONUSERBASE/bin:$PATH
#export PYTHONPATH\
#=$PYTHONUSERBASE/lib/python3.9/site-packages:$PYTHONPATH

# run ONETEP through python-ASE
python3 pt13_geo_opt_ase.py > pt13_geo_opt_ase_out.log

In this calculation, we used Ensemble-DFT as this is a metallic system. Theory and information on how to set Ensemble-DFT parameters can be found in the relevant section of the ONETEP manual. We remind the reader that in simple terms, geometry relaxation is a series of single point energy calculations. The structure for which we calculate the energy at every step is generated based on an optimisation algorithm. In this example, we performed geometry relaxation as a series of single point energy calculations and this is why the task is set to \(\mathrm{SinglePoint}\) in the ASE input. Then, the search direction, step size, and ultimately, the next step that corresponds to an atomic configuration are calculated through ASE’s built-in optimisation algorithm of choice. In this example, we used the \(\mathrm{ScipyFminBFGS}\) optimisation algorithm available in ASE [ase_optimizers_website]. In contrast with the previous example, the python output file now contains useful information about the optimisation process. This is of the form of,

              Step  Time        Energy      fmax
SciPyFminBFGS: 0  10:01:57  -46453.524595  2.0483
SciPyFminBFGS: 1  10:30:45  -46454.197133  1.7570
SciPyFminBFGS: 2  11:13:25  -46455.317379  0.9590
SciPyFminBFGS: 3  11:52:19  -46455.610507  0.4268
SciPyFminBFGS: 4  12:23:07  -46455.622235  0.0579
SciPyFminBFGS: 5  12:54:25  -46455.624640  0.0093

where, the optimisation algorithm is \(\mathrm{SciPyFminBFGS}\), the actual time, \(\mathrm{Time}\), that the calculation of the step has finished (this uses the time on the computer) is recorded, the \(\mathrm{Energy}\) is shown in units defined in ASE (these are \(\mathrm{eV}\) by default), and the maximum force magnitude on any atom in the system, \(\mathrm{fmax}\), is provided in units defined in ASE (these are \(\mathrm{eV \cdot}\) Å \(^{-1}\) by default). The trajectory of atomic positions is also printed in files \(\mathrm{opt.traj}\) and \(\mathrm{opt\_traj.xyz}\). The latter can be visualised with popular visualisation software. The relaxed geometry of this system is shown in Fig. 9.

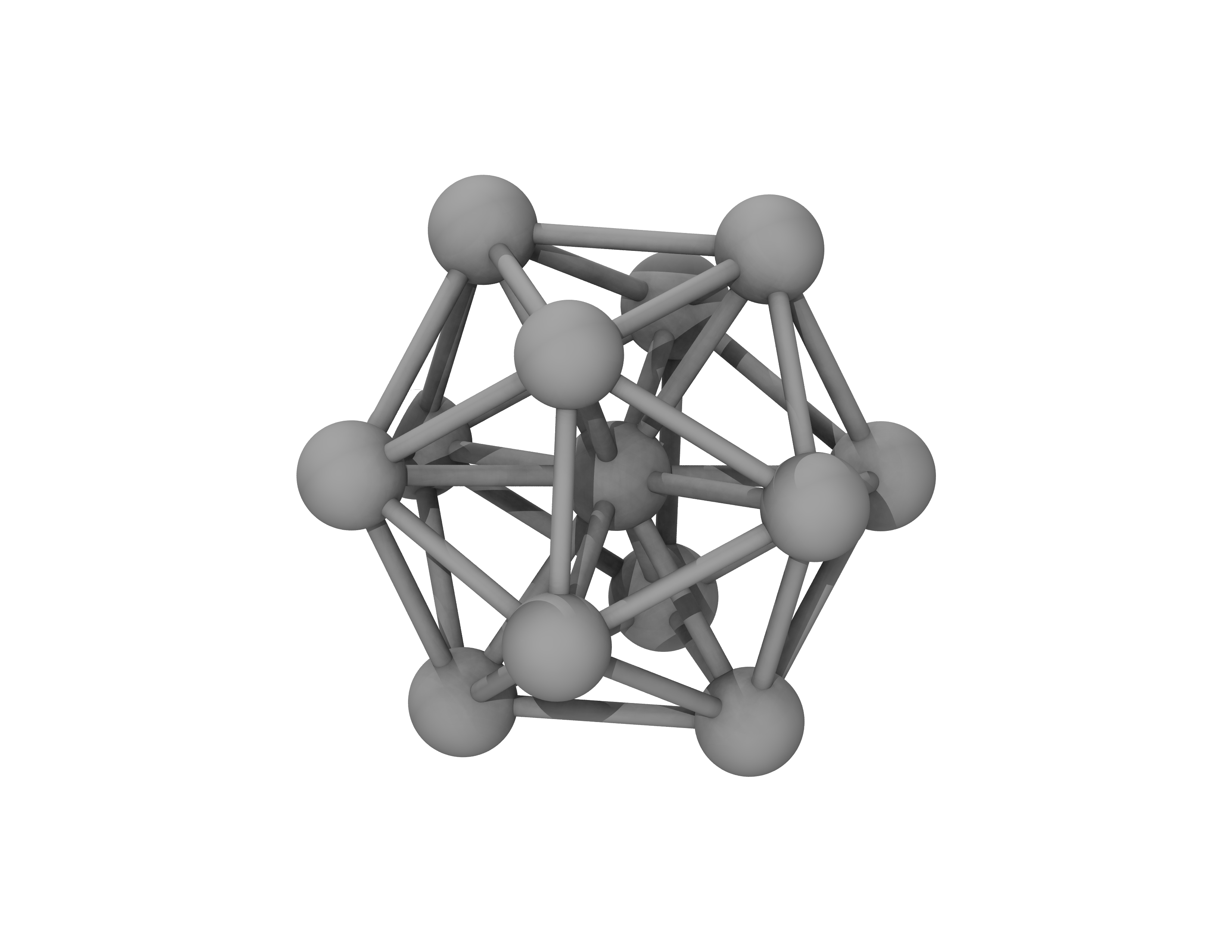
Fig. 9 Atomic configuration of the platinum nanoparticle after relaxing its geometry in ONETEP.

Summary

In this guide, we explained how to perform geometry relaxation in ONETEP. This can be achieved using either ONETEP or ASE built-in optimisation algorithms. This way we can obtain more stable structures than our initial guess for a given system. This is fundamental in chemistry as it can lead to many conclusions. First, we can obtain more accurate reaction energies by optimising the reactant and product geometries, and then calculate their energies. Additionally, we understand how different atomic arrangements affect the energy of the system and this is significant to a number of fields including and not limited to separations, catalysis, and biological phenomena.

Acknowledgement

We would like to thank Drs. Manuel Dos Santos Dias and Jacek Dziedzic for their suggestions after reading this manual. Also, we would like to thank Mr. Julian O. Holland for testing the ONETEP/ASE interface and for providing us with useful feedback.

[Scherlis2006]

D. A. Scherlis, J.-L. Fattebert, F. Gygi, M. Cococcioni, N. Marzari, “A unified electrostatic and cavitation model for first-principles molecular dynamics in solution”, J. Chem. Phys. 2006, 124, 074103.

[Schlegel2011]

H. B. Schlegel, “Geometry optimization”, WIREs Comput. Mol. Sci. 2011, 1, 790.

[Liu1989] (1,2)

D. C. Liu and J. Nocedal, “On the Limited Memory BFGS method for large scale optimization”, Math. Program. 1989, 45, 503.

[Pfrommer1997] (1,2)

B. G. Pfrommer, M. Cote, S. G. Louie, and M. L. Cohen, “Relaxation of Crystals with the Quasi-Newton Method”, J. Comput. Phys. 1997, 131, 233.

[Andzelm2001]

J. Andzelm, R. D. King-Smith, G. Fitzgerald, “Geometry optimization of solids using delocalized internal coordinates”, Chem. Phys. Lett. 2001, 335, 321.

[Barzilai1988]

J. Barzilai and J. M. Borwein, “Two-Point Step Size Gradient Methods”, IMA J. Numer. Anal. 1988, 8, 141 (1988).

[Aarons] (1,2,3,4)

J. Aarons, “A new CASTEP and ONETEP Geometry Optimiser” http://www.hector.ac.uk/cse/distributedcse/reports/castep-geom/castep-geom/HTML/dCSE_project.html.

[onetep_ase_interface]

https://wiki.fysik.dtu.dk/ase/ase/calculators/onetep.html. Copyright 2022, ASE-developers.

[ase_optimizers_website] (1,2)

https://wiki.fysik.dtu.dk/ase/ase/optimize.html. Copyright 2022, ASE-developers.

[Wolfe1969]

P. Wolfe, “Convergence conditions for ascent methods”, SIAM Rev. 1969, 11, 226.

[Wolfe1971]

P. Wolfe, “Convergence conditions for ascent methods. II: Some corrections”, SIAM Rev. 1969, 13, 185

[Gilbert1997] (1,2,3)

J. C. Gilbert, “On the realization of the Wolfe conditions in reduced quasi-Newton methods for equality constrained optimization”, SIAM J. Optim. 1997, 7, 780.

[Yuan2017] (1,2,3)

G. Yuan, Z. Wei, X. Lu, “Global convergence of BFGS and PRP methods under a modified weak Wolfe-Powell line search”, Appl. Math. Model. 2017, 47, 811.

[Avogadro]

Avogadro: an open-source molecular builder and visualisation tool. Version 1.95.1. http://avogadro.cc/

[Hanwell2012]

Avogadro: an open-source molecular builder and visualisation tool. Version 1.XX. http://avogadro.cc/ Marcus D Hanwell, Donald E Curtis, David C Lonie, Tim Vandermeersch, Eva Zurek and Geoffrey R Hutchison; “Avogadro: An advanced semantic chemical editor, visualisation, and analysis platform” Journal of Cheminformatics 2012, 4:17.

[ASE_nanoparticle]

https://wiki.fysik.dtu.dk/ase/ase/cluster/cluster.html. Copyright 2022, ASE-developers.

[Packwood2016] (1,2)

D. Packwood, J. Kermode, L. Mones, N. Bernstein, J. Woolley, N. Gould, C. Ortner, and G. Csányi, “A universal preconditioner for simulating condensed phase materials”, J. Chem. Phys. 2016, 144, 164109.

[Mones2018]

L. Mones, G. Csányi, and C. Ortner, “Preconditioners for the geometry optimisation and saddle point search of molecular systems”, ArXiv 2018, 1804.01590.

[Byrd1994]

R. H. Byrd, J. Nocedal, and R. B. Schnabel, “Representations of quasi-Newton matrices and their use in limited memory methods”, Math. Program 1994, 63, 129.

[CASTEP]

S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson, M. C. Payne, “First principles methods using CASTEP”, Z. Kristallogr. 2005, 220, 567.

[Pickard2006]

C. J. Pickard, “On-the-fly pseudopotential generation in CASTEP”, 2006 https://www.tcm.phy.cam.ac.uk/castep/otfg.pdf