Simulation Cell Relaxation

These notes describe the usage and functionality implemented in ONETEP for the calculation of the stress tensor and related quantities.

User guide

Table 7 Keywords table

Keyword	Type	Default	Description
STRESS	Task	—	Enable stress functionality.
stress_tensor	Logical	F	Enable the calculation of the stress tensor.
stress_elasticity	Logical	F	Enable the calculation of elastic constants
stress_relax	Logical	F	Use the stress tensor to optimise the cell parameters.
stress_assumed_symmetry	String	nosymm	Use assumed symmetry to minimise calculations. Values are nosymm; 3D: cubic ortho, tetra1, tetra2 hexa3d, rhomb1, rhomb2; 2D: recta, squar1, squar2, hexa2d NOTE: Symmetry is assumed, the code will not check if it’s correct!
stress_rescale_volume	Real	1.0	Rescaling for cell volume. Might be useful for 1D or 2D systems.
stress_components	Logical	T T T	Which rows/columns of the stress tensor to compute. The flags match X Y Z.
stress_deformation_step	Real	2.0e-3	Unitless strain parameter in finit difference It controls how different the deformation matrix is from the identity
stress_maxit_ngwf_cg	Integer	10	Maximum number of NGWF CG iterations for total energy calculations of distorted cells needed for the stress tensor.
stress_relax_energy_tol	Physical	1.0e-6 Ha	Convergence criterion for absolute change of energy in cell relaxation.
stress_relax_pressure	Physical	0.0 Ha/Bohr**3	External pressure applied during cell. relaxation
stress_relax_pressure_tol	Physical	2.0e-6 Ha/Bohr**3	Convergence criterion for absolute change of pressure in cell relaxation
stress_relax_cell_rtol	Real	1.0e-3	Convergence criterion for relative change of c cell parameters in cell relaxation.
stress_relax_max_iter	Integer	10	Maximum number of iterations in cell relaxation
stress_relax_max_step	Real	0.01	Maximum step size for distortion in cell relaxation.
stress_relax_atoms	Logical	F	Atomic positions are relaxed together with cell parameters.

The keywords table lists the input parameters that are available in connection with the stress implementation. The main functionality can be enabled by specifying the corresponding keyword (stress_tensor, stress_elasticity or stress_relax) without providing additional options. If the default values of the unspecified options are found to be unsuitable for the target system they can be overridden with the corresponding keyword in the input file.

The STRESS task gives access to all the features of the stress implementation. It first performs a standard self-consistent calculation for a reference unit cell (as given in the input file), and then performs subsequent calculations according to the requested stress-related quantities. This can be sped up quite considerably by writing out the density kernel (write_denskern T) or Hamiltonian (write_hamiltonian T) and NGWFs (write_tightbox_ngwfs T) files at the end of the self-consistent calculation for the reference unit cell. These should then be read for the calculations of the distorted structures used in constructing the stress tensor (read_denskern T, read_tightbox_ngwfs T and read_hamiltonian T). The code makes sure that the distorted cell calculations do not overwrite these files; if one is performing a cell relaxation calculation then these files can be updated by the self-consistent calculation for each new trial unit cell. Empirical observation: performing cell relaxation using only write_tightbox_ngwfs T shows the most stable and robust behaviour for the test calculations that I performed so far.

Calculation of the stress tensor

The definition for the stress tensor is

\[\sigma_{\alpha\beta} = -\frac{1}{V}\frac{\partial E}{\partial \epsilon_{\alpha\beta}} \;.\]

Here \(V\) is the volume of the unit cell, \(E\) is the total energy (of the unit cell), \(\sigma\) and \(\epsilon\) are the stress and strain tensors, respectively, and \(\alpha,\beta = x,y,z\). To convert to experimental units: energy divided by volume has units of pressure. The strain tensor describes a deformation of space away from a reference configuration: \(r_\alpha' = \left(\delta_{\alpha\beta} + \epsilon_{\alpha\beta}\right) r_\beta\) (Einstein summation convention) or \({\mathbf{r}}' = \left(1 + \epsilon\right) {\mathbf{r}}\). For more details see Section Background — Definition of stress for a crystal.

The stress tensor is calculated starting from a self-consistent calculation for a reference unit cell, applying distortions to those reference cell vectors, and using the corresponding total energy differences to approximate the derivatives of the total energy with respect to the distortion parameters. This is available through the STRESS task by setting stress_tensor to T.

Here are two examples of distortion matrices:

\[\begin{split}\epsilon_{xx}^- = \begin{pmatrix} 1 + h & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \;,\quad \epsilon_{xy}^+ = \begin{pmatrix} 1 & +h & 0 \\ +h & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \;.\end{split}\]

These act on the matrix of cell vectors as e.g.

\[\begin{split}\begin{pmatrix} a_{1x}' & a_{2x}' & a_{3x}' \\ a_{1y}' & a_{2y}' & a_{3y}' \\ a_{1z}' & a_{2z}' & a_{3z}' \end{pmatrix} = \begin{pmatrix} 1 & +h & 0 \\ +h & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} a_{1x} & a_{2x} & a_{3x} \\ a_{1y} & a_{2y} & a_{3y} \\ a_{1z} & a_{2z} & a_{3z} \end{pmatrix} \;.\end{split}\]

The parameter \(h\) is controlled by the keyword stress_deformation_step. As \(|h| \ll 1\), if the calculation for the distorted structure is started from the converged ground state obtained for the reference structure it should converge in a handful of iterations; stress_maxit_ngwf_cg can be used to control this and avoid spending too many iterations on a calculation that may have incorrect input and so takes too long to converge.

The stress tensor is a \(3\times3\) symmetric matrix, so it has 6 independent components. Finding all these components then requires 12 calculations for distorted cells (\(+h\) and \(-h\)), to form the centred differences that approximate the total energy derivatives. This can be alleviated if the unit cell is expected to have a definite symmetry. For example, for a cubic crystal \(\sigma_{xx} = \sigma_{yy} = \sigma_{zz} \neq 0\) and \(\sigma_{xy} = \sigma_{yz} = \sigma_{zx} = 0\), so only two distortions are needed (\(\epsilon_{xx}^+\) and \(\epsilon_{xx}^-\)). The keyword stress_assumed_symmetry controls the available options; see Table for a quick conversion and Table I of Ref. for the notation and further details. NOTE: Symmetry is assumed, the code will not check if it’s correct!

The stress tensor components only make sense if the corresponding spatial directions have periodic boundary conditions, which is the case of a bulk crystal. The keyword stress_components gives control over this, and if any of its flags is F it will override stress_assumed_symmetry to use nosymm. For example, for a 2D material with periodic boundary conditions in \(x\) and \(y\) and open boundary conditions (or a thick vacuum region) in the \(z\) direction, respectively, one would specify T T F to skip calculation (and usage) of information that involves the \(z\) direction. As another example, consider a nanotube which is periodic in the \(z\) direction; this would correspond to the flags F F T. Lastly, the stress tensor should not be computed for something which is surrounded entirely by vacuum, such as a molecule.

cubic	ortho	tetra1	tetra2	hexa3d	rhomb1	rhomb2
\(m\bar{3}\), \(m\bar{3}m\)	\(mmm\)	\(4/mmm\)	\(4/m\)	\(6/mmm\), \(6/m\)	\(\bar{3}m\)	\(\bar{3}\)
recta	squar1	squar2	hexa2d
\(2mm\)	\(4mm\)	\(4\)	\(6\), \(6mm\)

Calculation of the elastic properties

This part is still being developed, it should not be used yet.

Optimisation of the cell parameters

The stress tensor can be used to optimise the cell parameters by minimising the total energy with the STRESS task. This feature is enabled by stress_relax T. It could also be integrated with the GEOMETRYOPTIMIZATION task (not implemented so far).

Let us consider for simplicity that the atomic positions are fixed (relative to the unit cell vectors). We start from a unit cell specified by the vectors \(\{{\mathbf{a}}_1, {\mathbf{a}}_2, {\mathbf{a}}_3\}\) and want to calculate the optimised vectors \(\{{\mathbf{a}}_1^*, {\mathbf{a}}_2^*, {\mathbf{a}}_3^*\}\) that minimise the energy of the system, and so for which the stress tensor vanishes, \(\sigma_{\alpha\beta}(\{{\mathbf{a}}_i^*\}) = 0\). We can relate the known input cell parameters to the unknown optimised ones by a strain matrix,

\[\begin{split}\begin{pmatrix} a_{1x}^* & a_{2x}^* & a_{3x}^* \\ a_{1y}^* & a_{2y}^* & a_{3y}^* \\ a_{1z}^* & a_{2z}^* & a_{3z}^* \end{pmatrix} = \begin{pmatrix} 1 + \epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \\ \epsilon_{xy} & 1 + \epsilon_{yy} & \epsilon_{yz} \\ \epsilon_{xz} & \epsilon_{yz} & 1 + \epsilon_{zz} \end{pmatrix} \begin{pmatrix} a_{1x} & a_{2x} & a_{3x} \\ a_{1y} & a_{2y} & a_{3y} \\ a_{1z} & a_{2z} & a_{3z} \end{pmatrix} \;.\end{split}\]

We then Taylor expand the total energy in the strain parameters,

\[E(\epsilon) \approx E(0) + \sum_{(\alpha\beta)}\epsilon_{\alpha\beta}\left.\frac{\partial E}{\partial\epsilon_{\alpha\beta}}\right|_{\epsilon = 0} + \frac{1}{2} \sum_{(\alpha\beta),(\alpha'\beta')} \epsilon_{\alpha\beta}\,\epsilon_{\alpha'\beta'} \left.\frac{\partial^2 E}{\partial\epsilon_{\alpha\beta} \partial\epsilon_{\alpha'\beta'}}\right|_{\epsilon = 0} \;.\]

For the stress to vanish we evaluate the first derivative w.r.t. the strain parameters and set it to zero:

\[0 = \left.\frac{\partial E}{\partial\epsilon_{\alpha\beta}}\right|_{\epsilon \neq 0} = \left.\frac{\partial E}{\partial\epsilon_{\alpha\beta}}\right|_{\epsilon = 0} + \sum_{(\alpha'\beta')} \epsilon_{\alpha'\beta'} \left.\frac{\partial^2 E}{\partial\epsilon_{\alpha\beta} \partial\epsilon_{\alpha'\beta'}}\right|_{\epsilon = 0} \;.\]

The first derivative of the total energy is approximated by centred differences, but this also provides enough information to approximate the diagonal part of the matrix of second derivatives (\(\alpha'\beta' = \alpha\beta\)). This leads to an approximate Newton-like step to solve for the strain parameters \(\epsilon_{\alpha\beta}\):

\[\epsilon_{\alpha\beta} = -\left.\frac{\partial E}{\partial\epsilon_{\alpha\beta}}\right|_{\epsilon = 0} \left(\left.\frac{\partial^2 E}{\partial\epsilon_{\alpha\beta}^2}\right|_{\epsilon = 0}\right)^{-1} \;,\]

which is implemented as the cell relaxation method for fixed atomic positions.

In practice the optimisation of the cell parameters will not converge in one iteration. The maximum number of iterations or trial unit cells is controlled by stress_relax_max_iter. The magnitude of the deformation is controlled by stress_relax_max_step, which ensures that \(|\epsilon_{\alpha\beta}|\) does not exceed the specified value. There are three convergence criteria that must be satisfied simultaneously. stress_relax_energy_tol ensures that the change in total energy per atom between consecutive trial unit cells is below a given value, stress_relax_pressure_tol checks that the pressure of the current unit cell is below a target value, and stress_relax_acell_tol monitors the relative change in cell parameters, \(\frac{\max |\Delta a_{i\alpha}|}{\max |a_{i\alpha}|}\).

The atomic positions can also be optimised in tandem with the cell parameters. This is enabled by the flag stress_relax_atoms. The calculation will start by first optimising the atomic positions with fixed cell parameters, and then it will create a guess at the cell parameters to try next. If all the convergence thresholds for the cell optimisation are met the calculation ends, otherwise it keeps iterating by reoptimising the atomic positions and then making a new guess for the cell parameters. The optimisation of the atomic positions proceeds in the same way as with the GEOMETRYOPTIMIZATION task, and the corresponding keywords/flags can be used to control the same aspects of that process.

External pressure can included during cell relaxation using stress_relax_pressure. This will be added to the diagonal elements of the stress tensor which are not set to zero by the assumed symmetry in the calculation. Positive values of pressure will lead to a compression of the unit cell volume.

Background — Definition of stress for a crystal

These notes follow the original papers by Nielsen and Martin [Nielsen1983] [Nielsen1985] [Nielsen1985b] and the discussion in Chapter 3 of the book of Martin [Martin2008]. The definition for the stress tensor is

\[\sigma_{\alpha\beta} = -\frac{1}{V}\frac{\partial E}{\partial \epsilon_{\alpha\beta}} \;.\]

Here \(V\) is the volume of the unit cell, \(E\) is the total energy (of the unit cell), \(\sigma\) and \(\epsilon\) are the stress and strain tensors, respectively, and \(\alpha,\beta = x,y,z\). To convert to experimental units: energy divided by volume has units of pressure. \(1 \text{GPa} = 10 \text{kbar} = 10^9 j/m^3\), so it’s enough to convert the energy to Joule and the volume to cubic meters.

The strain tensor describes a deformation of space away from a reference configuration: \(r_\alpha' = \left(\delta_{\alpha\beta} + \epsilon_{\alpha\beta}\right) r_\beta\) (Einstein summation convention) or \({\mathbf{r}}' = \left(1 + \epsilon\right) {\mathbf{r}}\). The way this works is easiest to understand in one dimension and for a one-particle wave function \(\Psi(x)\), defined in the interval \([0,L]\) which is the unit cell for this example. Suppose that the unit cell is stretched to \([0,L']\) with \(L' = \left(1 + \epsilon\right) L\), and so the wave function will also be stretched to \(\widetilde{\Psi}(x')\) with the coordinate in the stretched unit cell being related to the starting one by \(x' = \left(1 + \epsilon\right) x\). This is illustrated in Fig. 10. The wave function at the stretched coordinate is almost the same as the wave function at the unstretched coordinate,

\[\widetilde{\Psi}(x') = C\,\Psi((1 + \epsilon)^{-1}x') = C\,\Psi(x) \;,\]

where \(C\) is a constant to be determined. [This is usually horribly confusing; a function returns a specified output for a given input, so if we want to know what is the value of the wave function \(\widetilde{\Psi}\) at \(x'\) we need to first transform that to the input for the wave function \(\Psi\) that will generate the correct output.] The remaining difference is that the wave function has to be normalised to the unit cell,

\[\int_0^{L}\hspace{-0.5em}{\mathrm{d}}x\;|\Psi(x)|^2 = 1 \;\Longrightarrow\; \int_0^{L'}\hspace{-0.5em}{\mathrm{d}}x'\;|\widetilde\Psi(x')|^2 = \left(1 + \epsilon\right) C^2 \!\int_0^{L}\hspace{-0.5em}{\mathrm{d}}x\;|\Psi(x)|^2 \;,\]

and so the complete relation is \(\widetilde{\Psi}(x') = \left(1 + \epsilon\right)^{-1/2} \Psi((1 + \epsilon)^{-1}x')\). Intuitively, the volume element is changed as \({\mathrm{d}}x' = \left(1 + \epsilon\right) {\mathrm{d}}x\), so the normalisation is adjusted to compensate.

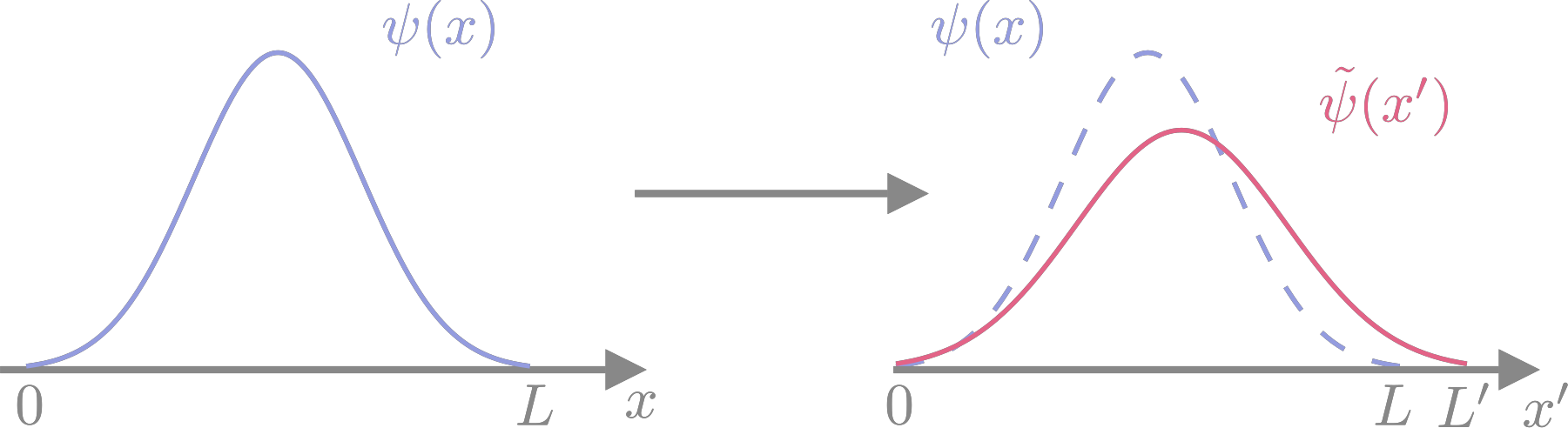
Fig. 10 One-dimensional example of coordinate stretching. Comparing the wave function in the stretched coordinate system to the one in the original coordinates shows that its centre (nuclear position) and its amplitude (normalisation) are both changed by the scaling

Moving now to the usual three-dimensional problem and to a crystalline setting, we first express the position vector in terms of the vectors defining the reference unit cell:

\[{\mathbf{r}} = r_1\,{\mathbf{a}}_1 + r_2\,{\mathbf{a}}_2 + r_3\,{\mathbf{a}}_3 \;.\]

In Cartesian coordinates this looks like

\[\begin{split}\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} a_{1x} & a_{2x} & a_{3x} \\ a_{1y} & a_{2y} & a_{3y} \\ a_{1z} & a_{2z} & a_{3z} \end{pmatrix} \begin{pmatrix} r_1 \\ r_2 \\ r_3 \end{pmatrix} \;.\end{split}\]

The transformation defining the action of the strain tensor \(\epsilon\) on the crystal can then be converted into a deformation of the unit cell:

(112)\[\]

The strain tensor is assumed symmetric; a skew-symmetric part would represent a homogeneous rotation of the whole crystal which should leave the energy invariant. The elements of the strain tensor have a simple interpretation when the unit cell vectors are proportional to the unit vectors defining the cartesian axes (e.g., orthorhombic cell): the diagonal elements \(\epsilon_{\alpha\alpha}\) (\(\alpha = x, y, z\)) represent a stretching or compression along the respective unit cell vector or cartesian axis (angles between the unit cell vectors are preserved), while the off-diagonal elements represent shear (the angle between the involved pair of unit cell vectors changes).

It is also common to map the subscripts to integers (Voigt notation),

\[\left(\epsilon_{xx}, \epsilon_{yy}, \epsilon_{zz}, 2\epsilon_{yz}, 2\epsilon_{xz}, 2\epsilon_{xy} \right) \rightarrow \left(\epsilon_1, \epsilon_2, \epsilon_3, \epsilon_4, \epsilon_5, \epsilon_6 \right) \;.\]

To understand how that factor of 2 propagates see the chapter on elasticity of Kittel’s book [Kittel] .

The strain can also be represented in a form which uses directly the unit cell vectors. Defining

\[{\mathbf{a}}_1^* = \frac{{\mathbf{a}}_2 \times {\mathbf{a}}_3}{V} \;,\quad {\mathbf{a}}_2^* = \frac{{\mathbf{a}}_3 \times {\mathbf{a}}_1}{V} \;,\quad {\mathbf{a}}_3^* = \frac{{\mathbf{a}}_1 \times {\mathbf{a}}_2}{V} \;,\quad {\mathbf{a}}_i \cdot {\mathbf{a}}_j^* = \delta_{ij} \;,\quad V = {\mathbf{a}}_1 \cdot \left({\mathbf{a}}_2 \times {\mathbf{a}}_3\right) \;,\]

we can write

\[\epsilon = \sum_{i,j} \epsilon_{ij}\,{\mathbf{a}}_i \otimes {\mathbf{a}}_j^* \;.\]

This is in general not a symmetric tensor in Cartesian components, but we enforce \(\epsilon_{ij} = \epsilon_{ji}\). It also only makes life easier if it acts on the matrix of cell vectors from the left,

\[\begin{split}\begin{aligned} \epsilon\,{\mathbf{a}}_1 &= \epsilon_{11}\,{\mathbf{a}}_1 + \epsilon_{12}\,{\mathbf{a}}_2 + \epsilon_{13}\,{\mathbf{a}}_3 \;, \\ \epsilon\,{\mathbf{a}}_2 &= \epsilon_{22}\,{\mathbf{a}}_2 + \epsilon_{12}\,{\mathbf{a}}_1 + \epsilon_{23}\,{\mathbf{a}}_3 \;, \\ \epsilon\,{\mathbf{a}}_3 &= \epsilon_{33}\,{\mathbf{a}}_3 + \epsilon_{13}\,{\mathbf{a}}_1 + \epsilon_{23}\,{\mathbf{a}}_2 \;.\end{aligned}\end{split}\]

The different elements can then be interpreted as effecting a stretch/compression of the respective unit cell vector (\(\epsilon_{ii}\)) or shears (\(\epsilon_{ij}\) with \(i \neq j\)), which bring cell vectors \(i\) and \(j\) towards/away from each other.

To be investigated:

\[\sigma = \sum_{i,j} \sigma_{ij}\,{\mathbf{a}}_i \otimes {\mathbf{a}}_j^* \;,\quad \sigma_{ij} = -\frac{1}{V}\frac{\partial E}{\partial \epsilon_{ij}} \;?\]

Computing the stress tensor

Ref. [Knuth2015] has nice derivations and a discussion of finite-difference tests in Section 4. For Projector Augmented Wave (PAW) specifics I looked at Ref. [Kresse1999] , but sadly they wrote “[…] it is also easy to evaluate the stress tensor. We will neither give the full derivation nor the final results here, as the expressions are rather cumbersome and difficult to write in a compact form.”

The straightforward numerical calculation by finite differences proceeds in the obvious way (here using the central difference formula):

\[\frac{\partial E_{\mathrm{tot}}}{\partial \epsilon_{\alpha\beta}} \approx \frac{E_{\mathrm{tot}}(\epsilon_{\alpha\beta} = +h) - E_{\mathrm{tot}}(\epsilon_{\alpha\beta} = -h)}{2h} \equiv \frac{\Delta E_{\mathrm{tot}}}{\Delta h} \;,\]

where the total energies are obtained from self-consistent calculations for the deformed unit cell with only one finite element in the strain tensor. The atomic positions should either be given in internal coordinates or otherwise their Cartesian coordinates have to be scaled. The unitless \(h\) has to be tuned via numerical tests, but values \(h < 0.01\) are mentioned as reasonable in Ref. [Knuth2015] ; for example Nielsen and Martin used \(h = 0.004\) [Nielsen1985b]. To fully populate the stress tensor using the central difference scheme for the general case one then requires 12 self-consistent calculations.

References

[Nielsen1983]

15. 8. Nielsen and R. M. Martin, First-principles calculation of stress, Phys. Rev. Lett. 50, 697 (1983).

[Nielsen1985]

15. 8. Nielsen and R. M. Martin, Quantum-mechanical theory of stress and force, Phys. Rev.B 32, 3780 (1985).

[Nielsen1985b] (1,2)

15. 8. Nielsen and R. M. Martin, Stresses in semiconductors: Ab initio calculations on Si, Ge, and GaAs, Phys. Rev. B 32, 3792 (1985)

[Martin2008]

18. 13. Martin, Electronic structure, 1st ed. (Cambridge Univ. Press, Cambridge, 2008)

[Kittel2004]

3. Kittel, Introduction to Solid State Physics, 8th ed. (Wiley, 2004).

[Knuth2015] (1,2)

6. Knuth, C. Carbogno, V. Atalla, V. Blum, and M. Scheffler, All-electron formalism for total energy strain derivatives and stress tensor components for numeric atom-centered orbitals, Comput. Phys. Commun. 190, 33 (2015)

[Kresse1999]

7. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B 59, 1758 (1999).