Electronic transport calculations

Author:: Robert A. Bell, University of Cambridge (rab207@cam.ac.uk)

Introduction

This document describes the use of the electronic transport functionality that is implemented in the ONETEP code [Bell2014]. The implementation computes the ballistic Landauer-Büttiker conductance at zero bias through a device and associated properties using electronic structure derived from density functional theory (DFT). The calculation proceeds as a post-processing step after a ground-state single-point calculation.

This document focuses on the practical aspects of setting up calculations; a detailed technical explanation of the method can be found in [Bell2014]. For a detailed discussion of the Landauer-Büttiker formalism and conductance derived from DFT see [DiVentra2008], [Datta1995].

I first briefly outline what is being calculated, I then give an example calculation and suitable input parameters, and then finally a full input parameter listing is given.

What is being calculated?

The transport calculation determines the ballistic conductance through a device. Current can flow between two leads via the connection made by the central scattering region. We will refer to this geometry as the device geometry.

Under the Landauer formalism, the contribution to the conductance between two leads (indexed \(i\) and \(j\)) from electrons with energy \(E\) is given by

\[G_{ij}(E) = \frac{2e^2}{h} T_{ij}(E)\]

where \(T_{ij}(E)\) is the transmission function. The transmission function is the central quantity to the Landauer-Büttiker conductance and is calculated using a Green’s function technique:

(62)\[ T_{ij}(E) = \mathrm{tr}\Big[\Gamma_i(E)\;G_{\rm d}(E)\;\Gamma_j(E)\;G_{\rm d}^{\dagger}(E)\Big],\]

(63)\[ G_{\rm d}(E) = \big[ (E+i\eta)S_{\rm d} - H_{\rm d} - \Sigma(E)\big]^{-1},\]

where \(H_{\rm d}\), \(S_{\rm d}\) the Hamiltonian and overlap matrices for the device, and \(\eta\) is an infinitessimal positive energy that selects the retarded response of the Green’s function \(G_{\rm d}\). The interaction with the semi-infinite leads accounted for through the lead self-energies \(\Sigma_j\), with \(\Sigma = \sum_j \Sigma_j\). The coupling matrices are defined as \(\Gamma_j = i(\Sigma_j - \Sigma_j^{\dagger})\).

From the Green’s function, one may also calculate the density of states within the device region as

\[\mathcal{N}(E) = -\frac{1}{\pi}{\mathrm{Im}}\mathrm{tr}\big[G_{\rm d}(E) S_{\rm d}\big].\]

Further post processing steps may be performed to determine the eigenchannels. [Bell2014], [Paulsson2007]

Building the device

The principal quantities required in Eqns. (62) and (63) are the device Hamiltonian and overlap matrices, and the lead self energies. The approach adopted in this implementation is to extract these matrix elements from the ground-state electronic structure obtained after a standard single-point calculation. This approach corresponds to a non-self consistent calculation of the transmission spectrum and device electronic structure. Note that this procedure differs from self consistent approaches, such as e.g. [Brandbyge2002], where the open boundary conditions of the leads are treated explicitly. At zero bias, however, both methods produce equivalent results yet the non-self consistent approach is often far less computationally expensive.

A detailed description of the matrix element extraction procedure, as implemented in the ONETEP code, is given in [Bell2014] which should be referred to in the first instance. Summarising briefly, to calculate the transmission through any device geometry the user must construct another auxilliary simulation structure that contains this device. The only electronic structure that is calculated is that of the auxilliary simulation geometry.

The structure of the auxilliary simulation geometry must take a specific form, consisting of the central region that connects the leads and a bulk-like region for each lead. Each lead region must have a local electronic structure that is bulk-like, and be large enough that it contains at least two principal layers of the bulk lead structure. [1] The device geometry is then defined as all the atoms contained within the central region and the two lead principal layers for each lead.

For a device connecting two leads, the device Hamiltonian then looks like

\[\begin{split}H_{\rm d} = \begin{pmatrix} \mathbf{h}_{00,L} & \mathbf{h}_{0,L} & \cdot & \cdot & \cdot \\ \mathbf{h}^\dagger_{01,L} & \mathbf{h}_{00,L} & \mathbf{h}_{LC} & \cdot & \cdot \\ \cdot & \mathbf{h}^\dagger_{LC} & \mathbf{h}_{C} & \mathbf{h}_{CR} & \cdot \\ \cdot & \cdot & \mathbf{h}^\dagger_{CR} & \mathbf{h}_{00,R} & \mathbf{h}_{01,R}\\ \cdot & \cdot & \cdot & \mathbf{h}^\dagger_{01,R} & \mathbf{h}_{00,R} \end{pmatrix}\end{split}\]

where \(\mathbf{h}_{00,L}\) is the on-site Hamiltonian block for the left lead principal layer, \(\mathbf{h}_{01,L}\) is the coupling Hamiltonian between principal layers, \(\mathbf{h}_{LC}\) is the coupling block between the left lead principal layer and the central region, and \(\mathbf{h}_{C}\) is the on-site block for the central region. As a result of the localisation of the NGWFs the device Hamiltonian takes the block tri-diagonal form, with zero matrix blocks denoted by a dot. An equivalent form is found for the device overlap matrix.

The lead self energies are computed using the \(\mathbf{h}_{00,L}, \mathbf{h}_{01,L}\) blocks via the method of Ref. [Lopez-Sancho1985]. Note that these blocks are contained within the device Hamiltonian \(H_{\rm d}\).

The device matrix elements are extracted from the electronic structure of the auxilliary simulation geometry. This procedure is entirely automated, however, and the user need only supply a list of atoms that define the device, and the subsets of these atoms that form the two principal layers for each lead. i.e. for an \(n\)-lead device, the user must define \(2n+1\) sets of atoms.

A single limitation of the implementation is that the two principal layers of any lead must be the exact same structure with atoms in the same relative ordering. This ensures that the lead self energies are computed correctly. The implementation will not do this automatically, however a check is performed to ensure that it is true before the calculation is started.

For a more detailed discussion of the procedure for extracting matrix elements see [Bell2014].

Setting up a calculation

The best way to explain how to set up an input is through an example, and here I give an explanation of the parameters required to calculation the transmission between two semi-infinite organic wires. Specifically, I will explain the setup for calculating the tunnelling current between a polyacetylene wire and polyyne wire where each wire is semi-infinite and terminated with a hydrogen atom. I will, however, assume that the user knows how to successfully converge the standard ONETEP single-point calculation.

A suitable auxiliary simulation geometry is shown in schematic form in Fig. 6, consisting of molecular fragments of the polyacetylene and polyyne wires located in vacuum. This entire geometry contains 52 atoms. I will assume that these atoms are ordered in the input file by their position from left to right.

Suppose that I wish to calculate the transmission spectrum in a \(\pm 2eV\) window about the Fermi energy with a resolution of \(0.01eV\). The transport specific input parameters are as follows:

etrans_lcr               : T
etrans_bulk              : T
etrans_emin              : -2.0 eV
etrans_emax              :  2.0 eV
etrans_enum              :  401
etrans_calculate_lead_mu : T

%block etrans_setup
  10  47
%endblock etrans_setup

%block etrans_leads
  10  17  18  25  unit_cells=2
  44  47  40  43  unit_cells=2
%endblock etrans_leads

! rest of input file...

The first six lines indicate that we wish to calculate the transmission between the two leads (the LCR transmision, see [Bell2014]), and the maximum transmission that could be injected by each lead (the bulk transmission), and the energy range the calculation will be performed over. I am also indicating that I want to calculate the lead band structures.

The first block after these six lines is the etrans_setup block which states that all atoms between atom \(10\) and \(47\) (inclusive, and in the order found in the input file) are defined as the device geometry. This region is given by the long-dashed box in . Atoms outside this set will not be included in the transmission calculation, but will be used when calculating the ground-state electronic structure.

The final block is the etrans_leads block which gives the subset of these device atoms that define the two principal layers for each lead. Each lead is given on a separate line, with the first pair of indices defining the principal layer furthest from the central region, and the second pair the principal layer closest to the central region. Note that this ordering of the two principal layers is important. Finally, I have indicated that each principal layer is in fact two primitive unit cells of the lead structure by using unit_cells=2. This tells ONETEP to symmetrise the lead matrix elements to reflect this periodicity. The atoms contained within each principal layer are indicated in by dotted boxes.

This choice of auxilliary simulation geometry tries to ensure that the lead principal layers are sufficiently far from the ends of the molecular fragments that the local electronic structure within the lead is bulk-like. This has required the use of buffer atoms (atoms 1–9 and 48–52) that are not included in the transport calculation. Some buffer has also been used between the principal layers and the central tunnelling gap (atoms 26–34 and 35–39) for the same reason. In practice, the size of this buffer is probably too small and the lead principal layers will not be well converged to the bulk. This can be tested by comparing the band structures of each lead to the corresponding bulk band structure for that lead, which can be calculated separately. If the lead band structure is not converged, the size of the buffer region should be increased.

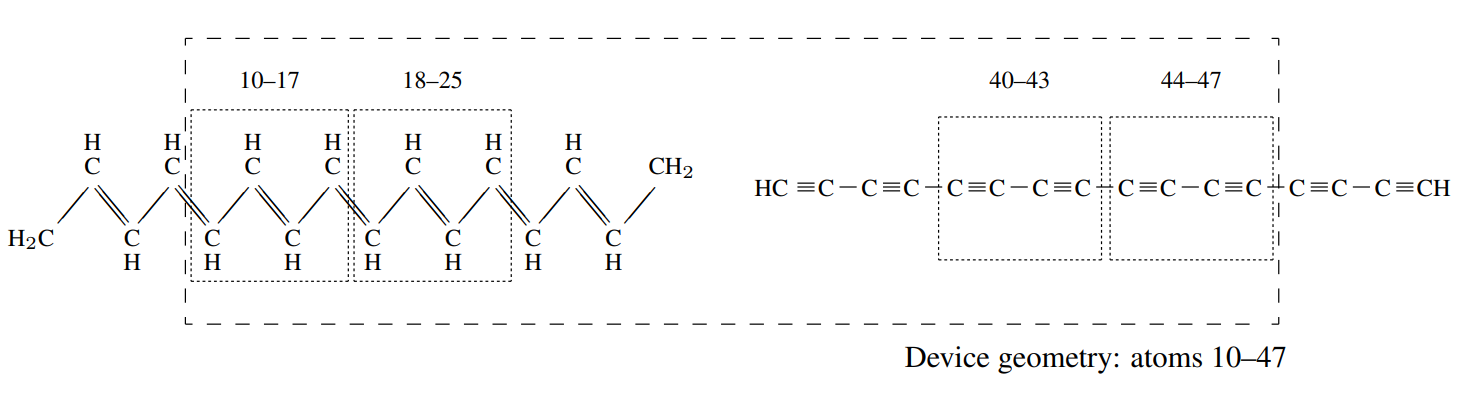
Fig. 6 A possible auxilliary simulation geometry for calculating the tunnelling transmission between a polyacetylene wire and a polyyne wire. The atoms appear ordered in the input file by their position from left to right.

Computational scaling

The dominant computationally-intensive task in the transport routines is the computing of the device Green’s function. This calculation is performed using an efficient block tri-diagonal Gaussian-elimination algorithm [Petersen2008]. This algorithm results in memory usage and operation counts that scale linearly in the number of atoms. The pre-factor to this scaling depends on the precise geometry of the device: the more one-dimensional a device (i.e. the fewer NGWFs that overlap), the lower this pre-factor.

Information on parallelisation

The calculation of transmission coefficients is parallelised over the energy points, with each MPI process performing the calculation in serial. No internal communications are necessary making the routines scale perfectly with the number of MPI processes. However, as all matrices must be replicated on each MPI process, the memory requirements can be large. On entering the transport routines but prior to starting the calculation, an estimate of the additional memory required by the transport routines is printed. Note that this estimate does not include the memory required by the rest of the ONETEP routines.

Parallelisation using OpenMP threading is not currently available. However, if the code is linked against Intel’s Math Kernel Library (MKL), the linear algebra routines can make use of multi-threading within this library. To do this, the flag -DMKLOMP must be included during compilation, and the number of threads can be set from the input file using threads_num_mkl.

The calculation of the eigenchannels can only be parallelised if linking against the ScaLAPACK library to make use of parallel dense algebra. To enable this, the flag -DSCALAPACK must be included at compilation.

Calculations using the joint NGWF basis

Transmission calculations using the joint (valence + conduction) NGWF basis set have often been found to be numerically unstable and produce qualitively incorrect results when compared to calculations using the valence NGWF basis alone. This is a result of ill-conditioning of the joint basis when the valence and conduction NGWFs are very similar in character. This is a known issue, however there is currently no fix.

For some systems it has been found that the valence NGWFs alone are capable of describing low-energy conduction states with good accuracy, and therefore the joint basis is not needed. It is advised that the valence basis is used in the first instance.

If you are certain that the joint basis is required, then proceed with caution and always compare the results generated with the joint basis to those generated using the valence basis. For energies below the Fermi energy, the two calculations should coincide. If they do not, or if errors (e.g. complaining about computing the transfer matrix/self energy, or lead band structures) are found then it may not be possible to use the joint basis.

If using the joint NGWF basis, all output files have .joint prepended to the extension.

Warnings and fixing errors

A useful check is to ensure that the lead band structure is as expected, and that the lead occupancy is correct. It is also useful to check the lead/device .xyz files to ensure that the leads have the expected geometry.

The following are the main warning messages that may be encountered, and how they may be tackled.

Inversion of (eS-H)_lcr failed: Cause: Failed to calculate the Green’s function as it is singular at this energy. This can happen if etrans_ecmplx is too small, or if localised states are present near this energy.

Severity: Low

Fix: It is safe to ignore this warning; the transmission coefficients and associated values are not written to file. If it occurs over a wide energy range, or in an energy range of interest, try increasing etrans_ecmplx.
Warning in compute_transfer: Failed to compute transfer matrix.: Cause: Failed to compute the lead self energy. This can happen if etrans_ecmplx is too small, or if localised states are present near this energy.

Severity: Low

Fix: It is safe to ignore this warning; the transmission coefficients and associated values are not written to file. If it occurs over a wide energy range, or in an energy range of interest, try increasing etrans_ecmplx. If using the joint NGWF basis, this may indicate that the basis is ill-conditioned and that the calculation is numerically unstable.
Lead electronic occupancy is significantly different ...: Cause: Large discrepancy between the ionic and electronic charge in the lead. Likely due to under-converged buffer region between this lead and the scattering region.

Severity: high

Fix: Check that the lead band structure is what is expected. Increase buffer region between the lead and the scattering region. Check the ground state DFT calculation is converged and that the density kernel occupancies are \(0\) or \(1\) (if using the default LNV algorithm).
Unable to determine lead potential for lead ...: Cause: lead potential calculation for this lead failed: could not determine the lead band structure. This may indicate that the leads have been defined incorrectly. Check the lead structure.

Severity: possibly high

Fix: Check the lead structure. Check the matrix elements contained in the lead .hsm output file are resonable, that the main weight is along the matrix diagonal and that the values are sensible. If using joint NGWF basis, try using the valence basis only (task = properties not properties_cond). The calculation will attempt to continue, but check carefully the results are as expected.

Full input parameter description

Main parameters

etrans_lcr: T/F [Logical, default etrans_lcr: F ]

Calculate the transmission spectrum between all pairs of leads in the system.

etrans_bulk: T/F [Logical, default etrans_bulk: F ]

Calculate the bulk transmission spectrum for the leads.

etrans_setup: [block]

%block etrans_setup

start end

%endblock etrans_setup

The block defining the atoms to be used in the transport calculation. start/end are integers giving the indices (from the input file) of the first/last atoms to be included as part of the system. All atoms between start and end are used in the calculation; atoms outside this range are buffer regions and ignored. The atoms consituting the leads must be contained within this region.

etrans_leads: [block]

%block etrans_leads

start0 end0 start1 end1

start0 end0 start1 end1 unit_cells=<n> file=<lead2.hsm>

...

%endblock etrans_leads

The block defining the atoms to be used as the leads. Each line defines a new lead. start0/end0 are integers giving the indices (from the input file) of the first/last atoms of the lead principal layer farthest from the central region; start1/end1 are integers giving the indices of the first/last atom of the principal later closest to the central region.

The first principal layer geometry must be a periodic repeat of the lead geometry (i.e. same number of atoms, in the same relative ordering in the input file).

For each lead, two optional tags can be defined. The option unit_cells=<n> forces the translational symmetry of the principal layer matrix elements, where n is the number of primitive unit cells in the principal layer. The option file=<lead1.hsm> allows for the lead matrix elements to be read in from a .hsm file. Reading in matrix elements is generally unnecessary, however it may be used effectively by taking the .hsm of a separate pristine/bulk transport calculation to ensure that the matrix elements are exactly at their bulk values. The positions and ordering of atoms in the lead principal layers in both calculations must be identical: this is not checked in the calculation.

etrans_enum: n [Integer, default etrans_enum: 50]

Number of transmission energy points calculated for. Energies are distributed uniformly.

etrans_emax : \(E_{\mathrm{max}}\) [Physical, default etrans_emax: -0.2 Hartree]

The maximum energy above the reference energy transmission is calculated for.

etrans_emin : \(E_{\mathrm{min}}\) [Physical, default etrans_emin: 0.2 Hartree]

The minimum energy below the reference energy transmission is calculated for.

etrans_eref_method: LEADS|REFERENCE|DIAG [String, default etrans_eref_method: LEADS]

The method used to determine the reference energy \(E_{\mathrm{ref}}\) for the transmission calculation.

If etrans_eref_method: LEADS, the reference energy is set as the average lead chemical potential.

If etrans_eref_method: DIAG, the reference energy is set as the Fermi energy of the original DFT system.

If etrans_eref_method: REFERENCE, the reference energy is set with etrans_eref.

If unset, this will be determined by calculating the average chemical potential of the leads, or if that calculation fails, the Fermi energy of the original DFT system will be used.

etrans_eref : \(E_{\mathrm{ref}}\) [Physical, default etrans_eref: Determined automatically]

Reference energy around which the transmission will be calculated. Energies are distributed uniformly in range \(E_{\mathrm{ref}}+E_{\mathrm{min}} \leq E \leq E_{\mathrm{ref}}+E_{\mathrm{max}}\).

This value is only used if etrans_eref_method : REFERENCE, otherwise it is determined automatically by the method given by etrans_eref_method.

etrans_num_eigchan : \(n_{\mathrm{chan}}\) [Integer, default etrans_num_eigchan: 0]

The number of eigenchannel transmissions calculated. The default does not decompose into eigenchannel transmissions.

etrans_plot_eigchan : T/F [Logical, default etrans_plot_eigchan: F]

Whether to plot the transmission eigenchannels of the LCR system.

etrans_plot_eigchan_energies : [block]

%block etrans_plot_eigchan_energies

{Ha|eV} ! optional energy unit

\(E_1\)

\(E_2\)

...

%endblock etrans_plot_eigchan_energies

The energies at which the eigenchannels are calculated and plotted. The first line may, optionally, define the energy unit; if undefined, the energy unit is Hartree.

Plotting the eigenchannels uses an algorithm that scales with the cube of the number of atoms in the LCR system. Compiling with the ScaLAPACK library is strongly recommended to reduce memory requirements.

etrans_write_xyz : T/F [Logical, default etrans_write_xyz : T]

Whether to write, separately, the lead and LCR geometries to file in the .xyz file format. This is useful for ensuring that the correct atoms have been chosen for the leads/LCR region.

Tweaking/optional parameters

etrans_ecmplx : \(\eta\) [Physical, default etrans_ecmplx: 1e-6 Hartree]

The small complex energy added to calculate the retarded Green’s function.

Ideally this should be infinitesimally small, however too small values create numerical instabilities. Large values improve numerical stability, but creates artificial scattering, reducing transmission.

etrans_calculate_lead_mu : T/F [Logical, default etrans_calculate_lead_mu: T]

Determine the chemical potential of the leads using a tight-binding approach. If etrans_eref is unset, the average lead chemical potential will be used as the reference energy. The band structure for each lead is saved to file basename_lead<nn>.bands.

etrans_num_lead_kpoints : \(n_k\) [Integer, default etrans_num_lead_kpoints: 32]

The number of lead band structure \(k\)-points sampled to determine the lead chemical potential. The \(k\)-points are distributed uniformly between \(\Gamma\) and \(X\).

etrans_same_leads : T/F [Logical, default etrans_same_leads: F]

Reuse the self energy from one lead for all leads. If all leads are identical, this may lead to a small computational saving. The saving is typically negligible however.

etrans_write_hs : T/F [Logical, default etrans_write_hs: F]

Write the lead Hamiltonian and overlap matrices to disk.

etrans_lead_disp_tol : \(\Delta r\) [Physical, default etrans_lead_disp_tol : 1.0 bohr]

The geometries of each lead and corresponding first principal layer should be identical; this parameter determines how strictly this is enforced. This should only be done if you are clear of the consequences.

This may be useful in the case that the lead unit cell is much larger than the NGWF radius. If the distance between the lead and the first principal layer furthest from the lead is much larger than 2 NGWF radii, these atoms do not directly influence the non-zero matrix elements between the principal layer and the lead, and the coupling matrix \(h_L\) is (approximately) independent of the structure of these atoms. Therefore, it may be possible to use a much smaller buffer region between the lead and the first principal layer by including part of the first principal layer in that buffer. The first principal layer and lead geometry need not be identical, however both regions must contain the same number of atoms and orbitals.

For each lead, the translation vector between the \(i^{th}\) atoms of the lead and first principal layer is calculated: \(\mathbf{R}_{i} = \mathbf{r}_{i\mathrm{,lead}} - \mathbf{r}_{i\mathrm{,PL}}\). If the geometries of the lead and first principal layer are identical, all of these translation vectors are identical. The maximum allowed difference between these displacement vectors is \(\Delta r > |\mathbf{R}_{i} - \mathbf{R}_{j}|\).

If the lead crosses the supercell boundary, this check will fail. This can be overridden by increasing \(\Delta r\) to some very large value.

etrans_lead_size_check : T/F [Logical, default etrans_lead_size_check: T]

If true, a check is performed to ensure that each lead forms complete principal layer. The run will abort if the periodic length of the lead unit cells, as defined in the input file, are smaller than twice the maximum NGWF radius of the species in that lead.

Turning off this check is not advised as the lead band structure and self energies can be inaccurate. This can also be a problem in situations where the left lead can interact with the principal layer of the right lead, allowing current to flow between the leads in the wrong direction, bypassing the central scattering region.

etrans_seed_lead [Integer, default etrans_seed_lead: 1]

The lead used to seed the block tri-diagonal partitioning. This should only be relevant for devices with more than two leads where one lead is much larger than the other leads.

threads_num_mkl [Integer, default threads_num_mkl: 1]

If the code is linked against Intel’s Math Kernel Library (MKL), this defines the number of threads used in the linear algebra routines. The flag -DMKLOMP must be set during compilation to enable this parameter, otherwise it is ignored.

Output file description

Output files contain self-explanatory headers for each column. For spin polarised calculations, a separate file is outputted for each spin channel.

basename_LCR.TRC

The LCR transmission coefficients between different pairs of leads of the system.

basename_LCR_channels_lead<nn>.TRC

The LCR transmission coefficients decomposed into eigenchannels. The lead number defines which lead acts as the source.

basename_LCR_E<nn>_lead<mm>_chan<ll>_{real\|imag}.cube

The plotted LCR eigenchannel. \(nn\) is the the energy index from %block etrans_plot_eigchan_energies; \(mm\) is the lead that acts as the source; \(ll\) is the eigenchannel number. The real and imaginary part are printed separately.

basename_BULK.TRC

The bulk transmission coefficients for each lead of the system.

basename_LCR.DOS

The density of states for the LCR system.

basename_BULK.DOS

The density of states for each lead of the system.

basename_lead<nn>.bands

Bandstructure of the lead in the .bands format. The number of \(k\)-points is set with etrans_num_lead_kpoints.

basename_device.xyz basename_lead<nn>.xyz

The geometries of the device and leads in .xyz file format.

basename_lead<nn>.hsm

The lead matrix elements in Fortran (unformatted) binary format. Note that all energies are in Hartree. It is planned, but currently not possible, to be able to access the device matrix elements. Please contact the developers if you are interested in using this functionality. The format of this file is
character(len=*) :: block_type  ! always lead
character(len=*) :: ham_type    ! valence or joint
integer          :: nspin       ! number of spin channels
integer          :: orbs(4)     ! NGWF indices corresponding
                                ! to the atoms defined
                                ! in block_etrans_leads
integer          :: norb        ! matrix sizes
real(kind=8)     :: eref        ! the lead chemical potential

real(kind=8)   :: h00(norb,norb,nspin)
real(kind=8)   :: h01(norb,norb,nspin)
real(kind=8)   :: s00(norb,norb)
real(kind=8)   :: s01(norb,norb)

[Bell2014] R.A. Bell, S.M.-M. Dubois, M.C. Payne, A. A. Mostofi, in preparation (2014)

[DiVentra2008] M. Di Ventra, Electrical Transport in Nanoscale Systems, (Cambridge University Press, Cambridge 2008)

[Datta1995] S. Datta, Electronic Transport in Mesoscopic System, 2nd ed. (Cambridge University Press, Cambridge 1995)

[Paulsson2007] M. Paulsson, M. Brandbyge, Phys. Rev. B. 76 115117 (2007)

[Lopez-Sancho1985] M.P. Lopez-Sancho, J.M. Lopez-Sancho, J. Rubio, J. Phys. F: Met. Phys. 15, 851 (1985)

[Petersen2008] D.E. Petersen et al., J. Comp. Phys 227, 3174 (2008)